
分析 根据新定义,逐项计算式子的两端,验证是否相等.
解答 解:对于(1),若向量$\overrightarrow a与\overrightarrow b$共线,则mq-np=0,∴$\overrightarrow a⊙\overrightarrow b=0$,故(1)正确;
对于(2),$\overrightarrow{b}$⊙$\overrightarrow{a}$=pn-qm,$\overrightarrow a⊙\overrightarrow b=mq-np$,故(2)不正确;
对于(3),($λ\overrightarrow{a}$)⊙$\overrightarrow{b}$=(λm,λn)⊙(p,q)=λmq-λnp,λ($\overrightarrow{a}$⊙$\overrightarrow{b}$)=λ(mq-np)=λmq-λnp.故(3)正确;
对于(4),($\overrightarrow{a}$⊙$\overrightarrow{b}$)2+($\overrightarrow{a}•\overrightarrow{b}$)2=(mq-np)2+(mp+nq)2=m2q2+n2p2+m2p2+n2q2=(m2+n2)(p2+q2),|$\overrightarrow{a}$|2=m2+n2,|$\overrightarrow{b}$|2=p2+q2,故(4)正确.
故答案为:(1),(3),(4).
点评 本题考查了平面向量的数量积运算和新定义运算,根据新定义计算是关键.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (-1,-$\frac{4}{5}$) | B. | (-1,$\frac{4}{5}$) | C. | (-1,$\frac{5}{4}$) | D. | (-1,-$\frac{5}{4}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
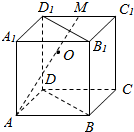
| A. | 三点D1,O,B共线,且OB=2OD1 | B. | 三点D1,O,B不共线,且OB=2OD1 | ||
| C. | 三点D1,O,B共线,且OB=OD1 | D. | 三点D1,O,B不共线,且OB=OD1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{2}{5}$ | B. | $\frac{1}{5}$ | C. | $\frac{3}{10}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com