练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    某几何体的三视图如图所示，该几何体的体积是______.

    解析试题分析：观察三视图可知，该几何体是一个直三棱柱，底面是一直角三角形，直角边长为a，三棱柱高为a，故其体积为=。
    考点：本题主要考查三视图，几何体的体积计算。
    点评：基础题，三视图是高考必考题目，因此，要明确三视图视图规则，准确地还原几何体，明确几何体的特征，以便进一步解题。三视图视图过程中，要注意虚线的出现，意味着有被遮掩的棱。

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：填空题

    如图，平面中两条直线l 1 和l 2相交于点O，对于平面上任意一点M，若x , y分别是M到直线l 1和l 2的距离，则称有序非负实数对（x , y）是点M的“ 距离坐标 ”。
    已知常数p≥0, q≥0，给出下列三个命题：
    ①若p=q=0，则“距离坐标”为（0，0）的点有且只有1个；
    ②若pq="0," 且p+q≠0，则“距离坐标”为( p, q) 的点有且只有2个；
    ③若pq≠0则“距离坐标”为 ( p, q) 的点有且只有3个.
    上述命题中，正确的有       . (填上所有正确结论对应的序号)
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    如图是一个几何体的三视图，根据图中数据，可得该几何体的体积是        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知某个几何体的三视图如图所示．根据图中标出的尺寸（单位：cm）．可得这个几何体的体积是        ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

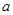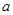    现有一个关于平面图形的命题：如图所示，同一个平面内有两个边长都是的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为，类比到空间，有两个棱长均为的正方体，其中一个的某顶点在另一个的中心，则这两个正方体重叠部分的体积恒为________．
     

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知三棱锥的所有顶点都在以为球心的球面上，是边长为的正三角形，为球的直径,若三棱锥的体积为，则球的表面积为       .

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    已知正方体的棱长为1，则它的外接球的表面积为_____     

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    正二十边形的对角线的条数是        ；

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    （文）将边长为的正方形沿对角线折起，使得平面平面，在折起后形成的三棱锥中，给出下列三个命题：
    ①是等边三角形； ②； ③三棱锥的体积是.
    其中正确命题的序号是______          ___。（写出所有正确命题的序号）

    查看答案和解析>>

    同步练习册答案