
分析 (1)求出二次函数的对称轴方程,讨论对称轴和区间[-1,1]的关系,运用函数的单调性即可得到最小值;
(2)设m<x1<x2<m+1,m为整数.分类讨论k的存在性,综合讨论结果,可得答案.
解答 解:(1)当b=$\frac{{a}^{2}}{4}$+1时,f(x)=(x+$\frac{a}{2}$)2+1,对称轴为x=-$\frac{a}{2}$,
当a≤-2时,函数f(x)在[-1,1]上递减,则g(a)=f(1)=$\frac{{a}^{2}}{4}$+a+2;
当-2<a≤2时,即有-1≤-$\frac{a}{2}$<1,则g(a)=f(-$\frac{a}{2}$)=1;
当a>2时,函数f(x)在[-1,1]上递增,则g(a)=f(-1)=$\frac{{a}^{2}}{4}$-a+2.
综上可得,g(a)=$\left\{\begin{array}{l}\frac{{a}^{2}}{4}+a+2,a≤2\\ 1,-2<a≤2\\ \frac{{a}^{2}}{4}-a+2,a>2\end{array}\right.$…(6分)
(2)设m<x1<x2<m+1,m为整数.
则△=a2-4b>0,即b<$\frac{{a}^{2}}{4}$,
①当-$\frac{a}{2}$∈(m,m+$\frac{1}{2}$],即-1≤a+2m<0时,
f(m)=m2+am+b<m2+am+$\frac{{a}^{2}}{4}$=(m+$\frac{a}{2}$)2≤$\frac{1}{4}$;
②当-$\frac{a}{2}$∈(m+$\frac{1}{2}$,m+1),即-2<a+2m<-1时,
f(m+1)=(m+1)2+a(m+1)+b<(m+2)2+a(m+1)+$\frac{{a}^{2}}{4}$=(m+1+$\frac{a}{2}$)2≤$\frac{1}{4}$;
综上,存在整数k,使得|f(k)|≤$\frac{1}{4}$.…(12分)
点评 本题考查的知识点是二次函数的图象和性质,分类讨论思想,熟练掌握二次函数的图象和性质,是解答的关键.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
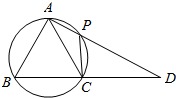 如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.
如图所示,在四边形ABCP中,线段AP与BC的延长线交于点D,已知AB=AC且A,B,C,P四点共圆.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2016 | B. | 2015 | C. | 2014 | D. | 2013 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 一条直线与两个平行平面中的一个相交,则必与另一个相交 | |
| B. | 平行于同一直线的两个平面平行 | |
| C. | 平行于同一平面的两个平面平行 | |
| D. | 一个平面与两个平行平面相交,交线平行 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com