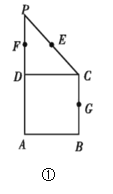
【题目】如图①在直角梯形ABCP中，
，
，
，
，E，F，G分别是线段PC，PD，BC的中点，现将
折起，使平面
平面ABCD如图②.
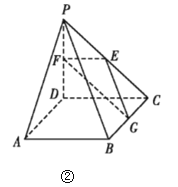
（1）求证:
平面EFG；
（2）求二面角G—EF—D的大小.
【答案】（1）证明见解析（2）
【解析】
(1) 以D坐标原点直线DADCDP分别为x,y与z轴建立空间直角坐标系,再计算平面
的法向量,证明
即可.
(2)根据(1)中建立的空间直角坐标系,利用空间向量求解二面角大小即可.
（1）在图②中,
平面
平面ABCD,平面
平面
, 
平面ABCD,
,如图以D坐标原点直线DADCDP分别为x,y与z轴建立空间直角坐标系,则有
,
,设平面GEF用法向量
,由法向量的定义得: 
,不妨设
,所以
,则
, 
点
平面EFG,
平面EFG.
（2）由（1）知平面GEF法向量,因平面EFD与坐标平面PDC重合,则它的一个法向量为
,设二面角G-EF-D为
,则由图观察二面角G-EF-D锐角, 
.故二面角G-EF-D的大小为.
解法二:（1）
,根据面面平行的判定定理, 
平面
平面PAB,又
面PAB, 平面EFG.
（2）平面平面ABCD,
, 
平面PCD,而
面EFD过C作
交
长线于R点连GR,根据三垂线定理知
即为二面角的平面角, 
,故二面角G-EF-D大小为.
科目：高中数学 来源： 题型：
【题目】一个口袋内装有大小相同的5个球，其中3个白球，2个黑球，从中一次摸出两个球．
（1）共有多少个基本事件？
（2）摸出的两个都是白球的概率是多少？
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物,我国PM2.5标准采用世界卫生组织设定的最宽限值,PM2.5日均值在35微克/立方米以下空气质量为一级;在35微克/立方米~75微克/立方米之间空气质量为二级;在75微克/立方米及其以上空气质量为超标.
某试点城市环保局从该市市区2016年全年每天的PM2.5监测数据中随机抽取6天的数据作为样本,监测值茎叶图(十位为茎,个位为叶)如图所示,若从这6天的数据中随机抽出2天,
(1)求恰有一天空气质量超标的概率;
(2)求至多有一天空气质量超标的概率.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】（1）已知双曲线的中心在原点，焦点在x轴上，实轴长为4，渐近线方程为
．求双曲线的标准方程；
（2）过（1）中双曲线上一点P的直线分别交两条渐近于
两点，且P是线段AB的中点，求证：
为常数；
（3）我们知道函数
的图象是由双曲线
的图象逆时针旋转45°得到的，函数
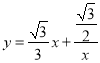的图象也是双曲线，请尝试写出曲线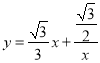的性质（不必证明）．
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
，如果对于定义域
内的任意实数
，对于给定的非零常数
，总存在非零常数
，恒有
成立，则称函数
是上的级类增周期函数，周期为，若恒有
成立，则称函数是上的级类周期函数，周期为.
（1）已知函数
是
上的周期为1的2级类增周期函数，求实数
的取值范围；
（2）已知
，是
上级类周期函数，且是上的单调递增函数，当
时，
，求实数的取值范围；
（3）是否存在实数
，使函数
是
上的周期为的级类周期函数，若存在，求出实数和的值，若不存在，说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知△
的三个内角
、
、
所对应的边分别为
、
、
，复数
，
，（其中
是虚数单位），且
.
（1）求证：
，并求边长的值；
（2）判断△的形状，并求当
时，角的大小.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知函数
，
的在数集
上都有定义，对于任意的
，当
时，
或
成立，则称是数集上的限制函数.
（1）求
在
上的限制函数的解析式；
（2）证明：如果在区间
上恒为正值，则在
上是增函数；[注：如果在区间上恒为负值，则在区间上是减函数，此结论无需证明，可以直接应用]
（3）利用（2）的结论，求函数
在
上的单调区间.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
