练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

     已知f（x）＝lg（－ax）是一个奇函数，则实数a的值是   （　　）

    A．1            B．－1          C．10           D．±1

     

    【答案】

     D解析：据题意知：f（x）＋f（－x）＝lg（－ax）＋lg（＋ax）＝0，

    即lg[（）2－（ax）2]＝lg[（1－a2）x2＋1]＝0，即（1－a2）x2＝0，而x不恒为0，

    则必有1－a2＝0⇒a＝±1，代入检验，函数定义域均关于原点对称．

     

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：013

    已知f（x）的定义域为（－∞，＋∞）且f（x＋2）＝f（x＋1）－f（x）且f（1）＝lg3－lg2，f（2）＝lg3＋lg5，则f（2003）的值为（    ）

    　　A．1

    　　B．－1

    　　C．lg　　 

    　　D．

     

    查看答案和解析>>

    科目：高中数学 来源：数学教研室 题型：013

    已知f（x）的定义域为（－∞，＋∞）且f（x＋2）＝f（x＋1）－f（x）且f（1）＝lg3－lg2，f（2）＝lg3＋lg5，则f（2003）的值为（    ）

    　　A．1

    　　B．－1

    　　C．lg　　 

    　　D．

     

    查看答案和解析>>

    科目：高中数学 来源：2014届北京市高一上学期期中考试数学 题型：解答题

    已知：集合M是满足下列性质的函数f（x）的全体：在定义域内存在x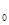，使得

    f（x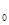＋1）＝f（x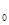）＋f（1）成立。

    （1）函数f（x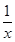）＝是否属于集合M？说明理由；

    （2）设函数f（x）＝lg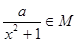，求实数a的取值范围；

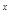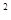
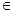    （3）证明：函数f（x）＝2＋xM。

     

    查看答案和解析>>

    科目：高中数学 来源：广东梅州市曾宪梓中学2010-2011学年高三10月考数学理 题型：选择题

     已知f（x）＝lg（－ax）是一个奇函数，则实数a的值是   （　　）

    A．1        B．－1          C．10           D．±1

     

    查看答案和解析>>

    同步练习册答案