
【题目】曲线C:ρ2﹣2ρcosθ﹣8=0 曲线E: ![]() (t是参数)
(t是参数)
(1)求曲线C的普通方程,并指出它是什么曲线.
(2)当k变化时指出曲线K是什么曲线以及它恒过的定点并求曲线E截曲线C所得弦长的最小值.
科目:高中数学 来源: 题型:
【题目】某市调研考试后,某校对甲、乙两个文科班的数学考试成绩进行分析,规定:大于或等于120分为优秀,120分以下为非优秀.统计成绩后,得到如下的![]() 列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为
列联表,且已知在甲、乙两个文科班全部110人中随机抽取1人为优秀的概率为![]() .
.
优秀 | 非优秀 | 合计 | |
甲班 | 10 | ||
乙班 | 30 | ||
合计 | 110 |
(1)请完成上面的列联表;
(2)根据列联表的数据,若按99%的可靠性要求,能否认为“成绩与班级有关系”;
(3)若按下面的方法从甲班优秀的学生中抽取一人:把甲班优秀的10名学生从2到11进行编号,先后两次抛掷一枚均匀的骰子,出现的点数之和为被抽取人的序号.试求抽到9号或10号的概率.
参考公式及数据:![]() ,
,![]() .
.
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数集A由实数构成:且满足:若![]() ,则
,则![]()
(1)若![]() ,试证明A中还有另外两个元素;
,试证明A中还有另外两个元素;
(2)集合A是否为双元素集合,并说明理由;
(3)若集合A是有限集,求集合A中所有元素的积。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,并且b=2
(1)若角A,B,C成等差数列,求△ABC外接圆的半径;
(2)若三边a,b,c成等差数列,求△ABC内切圆半径的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=2lnx+ ![]() ﹣2lna﹣k
﹣2lna﹣k ![]()
(1)若k=0,证明f(x)>0
(2)若f(x)≥0,求k的取值范围;并证明此时f(x)的极值存在且与a无关.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知等差数列{an}的前n项和为Sn , 若Sm﹣1=﹣4,Sm=0,Sm+2=14(m≥2,且m∈N*).
(1)求m的值;
(2)若数列{bn}满足 ![]() =logabn(n∈N*),求数列{(an+6)bn}的前n项和.
=logabn(n∈N*),求数列{(an+6)bn}的前n项和.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分14分)已知函数![]() .
.
(Ⅰ)若函数![]() 在其定义域上是增函数,求实数
在其定义域上是增函数,求实数![]() 的取值范围;
的取值范围;
(Ⅱ)当![]() 时,求出
时,求出![]() 的极值;
的极值;
(Ⅲ)在(Ⅰ)的条件下,若![]() 在
在![]() 内恒成立,试确定
内恒成立,试确定![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱台ABCD﹣A1B1C1D1中,底面ABCD为平行四边形,∠BAD=120°,M为CD上的点.且∠A1AB=∠A1AD=90°,AD=A1A=2,A1B1=DM=1. 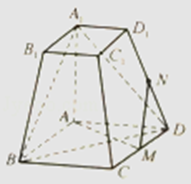
(1)求证:AM⊥A1B;
(2)若M为CD的中点,N为棱DD1上的点,且MN与平面A1BD所成角的正弦值为 ![]() ,试求DN的长.
,试求DN的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com