
����Ŀ��ijͬѧ��һ���о���ѧϰ�з��֣��������ʽ�ӵ�ֵ������ͬһ��������
1��sin213��+cos217�㩁sin13��cos17��
2��sin215��+cos215�㩁sin15��cos15��
3��sin218��+cos212�㩁sin18��cos12��
4��sin2����18�㣩+cos248�㩁sin2����18�㣩cos48��
5��sin2����25�㣩+cos255�㩁sin2����25�㣩cos55��
�����Դ��������ʽ����ѡ��һ����������������
�����ݣ��ļ�����������ͬѧ�ķ����ƹ�Ϊ���Ǻ��ʽ����֤����Ľ��ۣ�
���𰸡��⣺ѡ��2�����������£�
sin215��+cos215�㩁sin15��cos15��=1�� ![]() sin30��=
sin30��= ![]() ���� �������Ϊ
���� �������Ϊ ![]() ��
��
�����ݣ��ļ�����������ͬѧ�ķ����ƹ㣬�õ����Ǻ��ʽsin2��+cos2��30�㩁������sin��cos��30�㩁����= ![]() ��
��
֤����������һ��sin2��+cos2��30�㩁������sin��cos��30�㩁����=sin2��+ 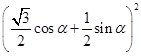 ��sin����cos30��cos��+sin30��sin����
��sin����cos30��cos��+sin30��sin����
=sin2��+ ![]() cos2��+
cos2��+ ![]() sin2��+
sin2��+ ![]() sin��cos����
sin��cos���� ![]() sin��cos����
sin��cos���� ![]() sin2��=
sin2��= ![]() sin2��+
sin2��+ ![]() cos2��=
cos2��= ![]() ��
��
����������sin2��+cos2��30�㩁������sin��cos��30�㩁����= ![]() +
+ ![]() ��sin����cos30��cos��+sin30��sin����
��sin����cos30��cos��+sin30��sin����
=1�� ![]() +
+ ![]() ��cos60��cos2��+sin60��sin2������
��cos60��cos2��+sin60��sin2������ ![]() sin2����
sin2���� ![]() sin2��
sin2��
=1�� ![]() +
+ ![]() cos2��+
cos2��+ ![]() sin2����
sin2���� ![]() sin2����
sin2���� ![]() =1��
=1�� ![]() ��
�� ![]() +
+ ![]() =
= ![]() ��
��
������������ѡ��2������sin215��+cos215�㩁sin15��cos15��=1�� ![]() sin30��=
sin30��= ![]() ���ɵ����������ֵ��
���ɵ����������ֵ��
�����ƹ㣬�õ����Ǻ��ʽsin2��+cos2��30�㩁������sin��cos��30�㩁����= ![]() ��֤������һ��ֱ���������Dz�����ҹ�ʽ�����ʽ����ߣ�����ɵý����
��֤������һ��ֱ���������Dz�����ҹ�ʽ�����ʽ����ߣ�����ɵý����
֤�������������ð�ǹ�ʽ�����Dz�����ҹ�ʽ��Ҫ���ʽ�ӻ�Ϊ ![]() +
+ ![]() ��sin����cos30��cos��+sin30��sin�������� 1��
��sin����cos30��cos��+sin30��sin�������� 1�� ![]() +
+ ![]() cos2��+
cos2��+ ![]() sin2��
sin2��
�� ![]() sin2����
sin2���� ![]() ������ɵý��
������ɵý��


 �������Ӧ���⼯ѵϵ�д�
�������Ӧ���⼯ѵϵ�д� �ۺ��Բ�ϵ�д�
�ۺ��Բ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ϵ�����������ֱ������ϵxOy�У�ԲC�IJ������� ![]() ����Ϊ����������OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��
����Ϊ����������OΪ���㣬x��ķǸ�����Ϊ���Ὠ��������ϵ��
��1����ԲC�ļ����귽�̣�
��2������OM����= ![]() ��ԲC�Ľ���ΪO��P���㣬��P��ļ����꣮
��ԲC�Ľ���ΪO��P���㣬��P��ļ����꣮
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��
��![]() ��
��![]() ����������Ϊ
����������Ϊ![]() ��
��![]() Ϊ��Բ
Ϊ��Բ![]() ��λ�ڵ�һ�����ڵ�һ��.
��λ�ڵ�һ�����ڵ�һ��.
��1������![]() ������Ϊ
������Ϊ![]() ������Բ
������Բ![]() �ı����̣�
�ı����̣�
��2����![]() Ϊ��Բ
Ϊ��Բ![]() ���㣬
���㣬![]() Ϊ��Բ
Ϊ��Բ![]() ��һ�㣬��
��һ�㣬��![]() ����ֱ��
����ֱ��![]() ��б��.
���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
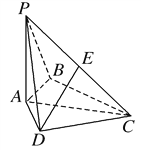
����Ŀ����ͼ��ʾ��������P��ABCD�У�����ABCDΪ���Σ�PA��ƽ��ABCD����E���߶�PC�ϣ�PC��ƽ��BDE��
��1��֤����BD��ƽ��PAC��
��2����PA=1��AD=2��������B��PC��A������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() �ֱ�����Բ
�ֱ�����Բ![]() �����ҽ��㣬������Ϊ
�����ҽ��㣬������Ϊ![]() ��
�� ![]() �ֱ�����Բ���ϡ��¶��㣬
�ֱ�����Բ���ϡ��¶��㣬 ![]() .
.
(1)����Բ![]() �ķ��̣�
�ķ��̣�
(2)��ֱ��![]() ����Բ
����Բ![]() ������������
������������![]() ��������ֱ��
��������ֱ��![]() ��б��֮��Ϊ
��б��֮��Ϊ![]() ��֤����ֱ��
��֤����ֱ��![]() ������㣬���ɶ��������.
������㣬���ɶ��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������![]() �У�
�У�![]() ƽ��
ƽ��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ���߶�
���߶�![]() ���е㣮
���е㣮
��1����֤��![]() ��ƽ��
��ƽ��![]() ��
��
��2��������![]() ������ֵ��
������ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڳ�����ABCD��A1B1C1D1�У�AB=1��BC=![]() ����M����CC1�ϣ���MD1��MA����MAD1�������Сʱ����CC1�ij�Ϊ��������
����M����CC1�ϣ���MD1��MA����MAD1�������Сʱ����CC1�ij�Ϊ��������

A. ![]() B.
B. ![]() C. 2 D.
C. 2 D. ![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD-A1B1C1D1���ⳤΪ1���߶�B1D1������������E��F����EF=![]() �� �����н����д���ĸ�����( )
�� �����н����д���ĸ�����( )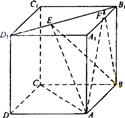
(1) AC��BE.
(2) ��PΪAA1�ϵ�һ��,��P��ƽ��BEF�ľ���Ϊ![]() .
.
(3) ����A-B![]() EF�����Ϊ��ֵ.
EF�����Ϊ��ֵ.
(4) �ڿռ���DD1,AC,B1C1���ཻ��ֱ����������.
(5) ��CC1���е���ֱ��AC1���ɽ�Ϊ40������ƽ��BEF���ɽ�Ϊ50��ֱ����2��.
A.0
B.1
C.2
D.3
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������˵����ȷ����
A. ���⡰![]() ���ķ�������
���ķ�������![]() ��
��
B. ���⡰��![]() ����
����![]() ���ķ�����Ϊ����
���ķ�����Ϊ����![]() ����
����![]() ��
��
C. ������![]() ����
����![]() ������
������![]() ������
������
D. ������ʵ������![]() ����������
����������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com