
【题目】![]() 两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
两个居民小区的居委会欲组织本小区的中学生,利用双休日去市郊的敬老院参加献爱心活动.两个校区每位同学的往返车费及服务老人的人数如下表:
|
| |
往返车费 | 3元 | 5元 |
服务老人的人数 | 5人 | 3人 |
根据安排,去敬老院的往返总车费不能超过37元,且![]() 小区参加献爱心活动的同学比
小区参加献爱心活动的同学比![]() 小区的同学至少多1人,则接受服务的老人最多有____人.
小区的同学至少多1人,则接受服务的老人最多有____人.
科目:高中数学 来源: 题型:
【题目】若无穷数列![]() 满足:
满足:![]() ,当
,当![]() ',
',![]() 时,
时,![]()
![]() (其中
(其中![]() 表示
表示![]() ,
,![]() ,…,
,…,![]() 中的最大项),有以下结论:
中的最大项),有以下结论:
① 若数列![]() 是常数列,则
是常数列,则![]() ;
;
② 若数列![]() 是公差
是公差![]() 的等差数列,则
的等差数列,则![]() ;
;
③ 若数列![]() 是公比为
是公比为![]() 的等比数列,则
的等比数列,则![]() :
:
④ 若存在正整数![]() ,对任意
,对任意![]() ,都有
,都有![]() ,则
,则![]() ,是数列
,是数列![]() 的最大项.
的最大项.
其中正确结论的序号是____(写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家环境标准制定的空气质量指数与空气质量等级对应关系如表:
空气质量指数 | 0~50 | 51~100 | 101~150 | 151~200 | 201~300 | 300以上 |
空气质量等级 | 1级优 | 2级良 | 3级轻 度污染 | 4级中度污染 | 5级重 度污染 | 6级严重污染 |
由全国重点城市环境监测网获得10月份某五天甲城市和乙城市的空气质量指数数据用茎叶图表示如图:
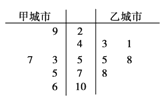
(1)试根据上面的统计数据,计算甲、乙两个城市的空气质量指数的方差;
(2)试根据上面的统计数据,估计甲城市某一天空气质量等级为2级良的概率;
(3)分别从甲城市和乙城市的统计数据中任取一个,试求两个城市空气质量等级相同的概率.供参考数据:292+532+572+752+1062=23760,432+412+552+582+782=16003
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校为了诊断高三学生在市“一模”考试中文科数学备考的状况,随机抽取了50名学生的市“一模”数学成绩进行分析,将这些成绩分为九组,第一组[60,70),第二组[70,80),……,第九组[140,150],并绘制了如图所示的频率分布直方图.

(1)试求出![]() 的值并估计该校文科数学成绩的众数和中位数;
的值并估计该校文科数学成绩的众数和中位数;
(2)现从成绩在[120,150]的同学中随机抽取2人进行谈话,那么抽取的2人中恰好有一人的成绩在[130,140)中的概率是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率为
的离心率为![]() ,焦点分别为
,焦点分别为![]() ,点
,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 面积的最大值是
面积的最大值是![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() 是椭圆
是椭圆![]() 上的点,
上的点,![]() 是坐标原点,若
是坐标原点,若![]() 判定四边形
判定四边形![]() 的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
的面积是否为定值?若为定值,求出定值;如果不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题中,假命题的个数是( )
(1)若直线a在平面![]() 上,直线b不在平面
上,直线b不在平面![]() 上,则a,b是异面直线;
上,则a,b是异面直线;
(2)若a,b是异面直线、则与a,b都垂直的直线有且只有一条
(3)若a,b是异面直线、若c,d与直线a,b都相交,则c,d也是异面直线
(4)设a,b是两条直线,若![]() 平面
平面![]() ,
,![]() ,则
,则![]() 平面
平面![]() .
.
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“文、明、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“文、明、中、国”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 013 320 122 103 233
由此可以估计,恰好第三次就停止的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】有![]() 名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
名学生排成一排,求分别满足下列条件的排法种数,要求列式并给出计算结果.
(1)甲不在两端;
(2)甲、乙相邻;
(3)甲、乙、丙三人两两不得相邻;
(4)甲不在排头,乙不在排尾。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com