
【题目】某“农家乐”接待中心有客房200间,每间日租金为40元,每天都客满.根据实际需要,该中心需提高租金,如果每间客房日租金每增加4元,客房出租就会减少10间.(不考虑其他因素)
(1)设每间客房日租金提高![]() 元(
元(![]() ),记该中心客房的日租金总收入为
),记该中心客房的日租金总收入为![]() ,试用
,试用![]() 表示
表示![]()
(2)在(1)的条件下,每间客房日租金为多少时,该中心客房的日租金总收入最高?
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .不过原点的直线
.不过原点的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() 两点,设直线
两点,设直线![]() ,直线
,直线![]() ,直线
,直线![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() 成等比数列.
成等比数列.
(1)求![]() 的值;
的值;
(2)若点![]() 在椭圆
在椭圆![]() 上,满足
上,满足![]() 的直线
的直线![]() 是否存在?若存在,求出直线
是否存在?若存在,求出直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】判断下列命题的真假.
(1)过一条直线的平面有无数多个;
(2)如果两个平面有两个公共点![]() ,那么它们就有无数多个公共点,并且这些公共点都在直线
,那么它们就有无数多个公共点,并且这些公共点都在直线![]() 上;
上;
(3)两个平面的公共点组成的集合,可能是一条线段;
(4)两个相交平面可能存在不在一条直线上的3个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列命题:
①过圆心和圆上的两点有且只有一个平面
②若直线![]() 与平面
与平面![]() 平行,则
平行,则![]() 与平面
与平面![]() 内的任意一条直线都没有公共点
内的任意一条直线都没有公共点
③若直线![]() 上有无数个点不在平面
上有无数个点不在平面![]() 内,则
内,则![]()
④如果两条平行线中的一条与一个平面平行,那么另一条也与这个平面平行
⑤垂直于同一个平面的两条直线平行
其中正确的命题的个数是![]()
![]()
A.1B.2C.3D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】通过随机询问![]() 名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
名不同性别的大学生在购买食物时是否看营养说明,得到如下列联表:
男 | 女 | 总计 | |
读营养说明 |
|
|
|
不读营养说明 |
|
|
|
总计 |
|
|
|
附:
|
|
|
|
|
|
|
|
![]()
(1)由以上列联表判断,能否在犯错误的概率不超过![]() 的前提下认为性别和是否看营养说明有关系呢?
的前提下认为性别和是否看营养说明有关系呢?
(2)从被询问的![]() 名不读营养说明的大学生中随机选取
名不读营养说明的大学生中随机选取![]() 名学生,求抽到女生人数
名学生,求抽到女生人数![]() 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点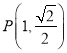 ,且离心率为
,且离心率为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,不经过
的左、右焦点,不经过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 交于两个不同的点
交于两个不同的点![]() ,如果直线
,如果直线![]() 、
、![]() 、
、![]() 的斜率依次成等差数列,求焦点
的斜率依次成等差数列,求焦点![]() 到直线
到直线![]() 的距离
的距离![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在2018年3月郑州第二次模拟考试中,某校共有100名文科学生参加考试,其中语文考试成绩低于130的占95%人,数学成绩的频率分布直方图如图:
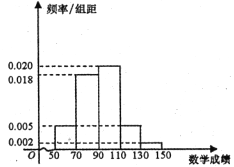
(Ⅰ)如果成绩不低于130的为特别优秀,这100名学生中本次考试语文、数学成绩特别优秀的大约各多少人?
(Ⅱ)如果语文和数学两科都特别优秀的共有3人.
(ⅰ)从(Ⅰ)中的这些同学中随机抽取2人,求这两人两科成绩都优秀的概率.
(ⅱ)根据以上数据,完成![]() 列联表,并分析是否有99%的把握认为语文特别优秀的同学,数学也特别优秀.
列联表,并分析是否有99%的把握认为语文特别优秀的同学,数学也特别优秀.
语文特别优秀 | 语文不特别优秀 | 合计 | |
数学特别优秀 | |||
数学不特别优秀 | |||
合计 |
![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年空气质量逐步恶化,雾霾天气现象出现增多,大气污染危害加重.大气污染可引起心悸、呼吸困难等心肺疾病.为了解某市心肺疾病是否与性别有关,在某医院随机对心肺疾病入院的![]() 人进行问卷调查,得到了如下的列联表:
人进行问卷调查,得到了如下的列联表:
患心肺疾病 | 不患心肺疾病 | 合计 | |
男 |
|
|
|
女 |
|
|
|
合计 |
|
|
|
(1)用分层抽样的方法在患心肺疾病的人群中抽![]() 人,其中男性抽多少人?
人,其中男性抽多少人?
(2)在上述抽取的![]() 人中选
人中选![]() 人,求恰好有
人,求恰好有![]() 名女性的概率;
名女性的概率;
(3)为了研究心肺疾病是否与性别有关,请计算出统计量![]() ,你有多大把握认为心肺疾病与性别有关?
,你有多大把握认为心肺疾病与性别有关?
下面的临界值表供参考:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
参考公式:  ,其中
,其中![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com