
思路解析:该二次函数的图象开口向下,因而若x∈R,则y=-(x-a)2+a2+a-2,即当x=a时,ymax=a2+a-2目前规定x∈[1,2],解题时应分a∈[1,2]以及a<1,a>2三种情况讨论(三种情况中最大值的取得均不同).
解:y=-x2+2ax+(a-2)=-(x-a)2+a2+a-2,
①若a∈[-1,2],则当x=a时,ymax=a2+a-2,由题意知a2+a-2=4,而a2+a-6=0,a=-3或a=2,
∵a∈[-1,2],∴a=2符合条件.
②若a<-1,
∵二次函数y=f(x)在[a,+∞)上单调递减,即在[-1,2]上单调递减,
∴当x=-1时,ymax=-1-2a+a-2=-a-3,由-a-3=4,得a=-7(<-1).
∴a=-7符合条件.
③若a>2,则二次函数y=f(x)在[-1,2]上单调递增,
∴当x=2时,ymax=-4+4a+a-2=5a-6.由5a-6=4,得a=2(≯2).
∴此时不存在符合条件的a.
综上,符合条件的a的值为2或-7.


 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案科目:高中数学 来源: 题型:
已知二次函数y=f(x)的图像经过坐标原点,其导函数为f??(x)=6x-2,数列{an}的前n项和为Sn,点(n,Sn)(n∈N*)均在函数y=f(x)的图像上.(Ⅰ)求数列{an}的通项公式;(Ⅱ)设bn=,Tn是数列{bn}的前n项和,求使得Tn<对所有n∈N*都成立的最小正整数m;
查看答案和解析>>
科目:高中数学 来源:2015届山东省高一暑假作业(一)数学试卷(解析版) 题型:解答题
已知二次函数y=f(x)(x∈R)的图像是一条开口向下且对称轴为x=3的抛物线,试比较大小:
(1)f(6)与f(4)
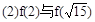
查看答案和解析>>
科目:高中数学 来源:2012年江苏省高一上学期开学考试数学 题型:填空题
已知二次函数y=ax2+bx+c(a≠0)的图象如图,则下列结论中正确的是 ;(填写正确的序号)
①a>0 ②当x>1时,y随x的增大而增大
③c<0 ④3是方程ax2+bx+c=0的一个根

第12题图
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com