
【题目】如图,甲、乙两个企业的用电负荷量![]() 关于投产持续时间
关于投产持续时间![]() (单位:小时)的关系
(单位:小时)的关系![]() 均近似地满足函数
均近似地满足函数![]() .
.
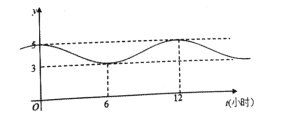
(1)根据图象,求函数![]() 的解析式;
的解析式;
(2)为使任意时刻两企业用电负荷量之和不超过9,现采用错峰用电的方式,让企业乙比企业甲推迟![]() 小时投产,求
小时投产,求![]() 的最小值.
的最小值.
科目:高中数学 来源: 题型:
【题目】 如图是正方体的平面展开图.在这个正方体中,
①BM∥平面DE;②CN∥平面AF;③平面BDM∥平面AFN;④平面BDE∥平面NCF.
以上四个命题中,正确命题的序号是________.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,已知四棱锥P-ABCD的底面为直角梯形,AB//DC,![]() ,PA
,PA![]() 底面ABCD,且PA=AD=DC=
底面ABCD,且PA=AD=DC=![]() AB=1,M是PB的中点.
AB=1,M是PB的中点.
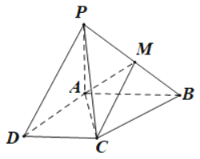
(1)证明:面PAD![]() 面PCD;
面PCD;
(2)求AC与PB所成角的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若![]() 是一个由数字1,2,3,4,5,6,7,8,9组成的
是一个由数字1,2,3,4,5,6,7,8,9组成的![]() 位正整数,并同时满足如下两个条件:
位正整数,并同时满足如下两个条件:
(1)数字1,2,…,![]() 在
在![]() 中各出现两次;
中各出现两次;
(2)每两个相同的数字![]() 之间恰有
之间恰有![]() 个数字.
个数字.
此时,我们称这样的正整数![]() 为“好数”.例如,当
为“好数”.例如,当![]() 时,
时,![]() 可以是312 132.试确定满足条件的正整数
可以是312 132.试确定满足条件的正整数![]() 的值,并各写出一个相应的好数
的值,并各写出一个相应的好数![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】近年来,“共享单车”的出现为市民“绿色出行”提供了极大的方便,某共享单车公司“Mobike”计划在甲、乙两座城市共投资120万元,根据行业规定,每个城市至少要投资40万元,由前期市场调研可知:甲城市收益P与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,乙城市收益Q与投入
,乙城市收益Q与投入![]() (单位:万元)满足
(单位:万元)满足![]() ,设甲城市的投入为
,设甲城市的投入为![]() (单位:万元),两个城市的总收益为
(单位:万元),两个城市的总收益为![]() (单位:万元).
(单位:万元).
(1)当甲城市投资50万元时,求此时公司总收益;
(2)试问如何安排甲、乙两个城市的投资,才能使总收益最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com