
【题目】随着经济的发展,个人收入的提高.自2018年10月1日起,个人所得税起征点和税率的调整.调整如下:纳税人的工资、薪金所得,以每月全部收入额减除5000元后的余额为应纳税所得额.依照个人所得税税率表,调整前后的计算方法如下表:
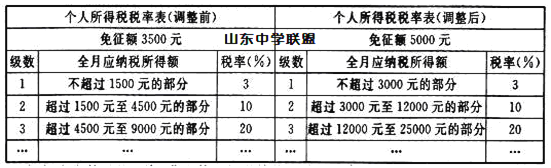
(1)小李该月的工资、薪金等税前收入为7500元时,请你帮小李算一下调整后小李的实际收入比调整前增加了多少?
(2)某税务部门在小李所在公司利用分层抽样方法抽取某月100个不同层次员工的税前收入,并制成下面的频数分布表:
![]()
先从收入在[3000,5000)及[5000,7000)的人群中按分层抽样抽取7人,再从中选4人作为新纳税法知识宣讲员,求两个宣讲员不全是同一收入人群的概率;
【答案】(1)220元(2)![]()
【解析】
(1)可得按调整前起征点应纳个税为1500×3%+2500×10%=295元,按调整后起征点应纳个税为2500×3%=75元,两者相减可得答案;
(2) 由频数分布表可知从[3000,5000)及[5000,7000)的人群中按分层抽样抽取7人,其中[3000,5000)中占3人,分别记为A,B,C,[5000,7000)中占4人,分别记为1,2,3,4,再从这7人中选2人的所有组合有21种情况,其中不在同一收入人群的有12种情况,由概率计算公式计算可得答案.
解:(1)由于小李的工资、薪金等收入为7500元,
按调整前起征点应纳个税为1500×3%+2500×10%=295元;
按调整后起征点应纳个税为2500×3%=75元,
比较两个纳税方案可知,按调整后起征点应纳个税少交220元,
即个人的实际收入增加了220元,所以小李的实际收入增加了220元。
(2)由频数分布表可知从[3000,5000)及[5000,7000)的人群中按分层抽样抽取7人,其中[3000,5000)中占3人,分别记为A,B,C,[5000,7000)中占4人,分别记为1,2,3,4,再从这7人中选2人的所有组合有:AB,AC,A1,A2,A3,A4,BC,B1,B2,B3,B4,C1,C2,C3,C4,12,13,14,23,24,34,共21种情况,
其中不在同一收入人群的有:Al,A2,A3,A4,B1,B2,B3,B4,C1,C2,C3,C4,共12种,所以所求概率为![]() .
.


科目:高中数学 来源: 题型:
【题目】某课题小组共10人,已知该小组外出参加交流活动次数为1,2,3的人数分别为3,3, 4,现从这10人中随机选出2人作为该组代表参加座谈会.
(1)记“选出2人外出参加交流活动次数之和为4”为事件A,求事件A发生的概率;
(2)设X为选出2人参加交流活动次数之差的绝对值,求随机变量X的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附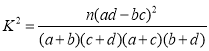 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公交公司为了方便市民出行、科学规划车辆投放,在一个人员密集流动地段增设一个起点站,为研究车辆发车间隔时间![]() (分钟)与乘客等候人数
(分钟)与乘客等候人数![]() (人)之间的关系,经过调查得到如下数据:
(人)之间的关系,经过调查得到如下数据:
间隔时间 |
|
|
|
|
|
|
等候人数 |
|
|
|
|
|
|
调查小组先从这![]() 组数据中选取
组数据中选取![]() 组数据求线性回归方程,再用剩下的
组数据求线性回归方程,再用剩下的![]() 组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数
组数据进行检验.检验方法如下:先用求得的线性回归方程计算间隔时间对应的等候人数![]() ,再求
,再求![]() 与实际等候人数
与实际等候人数![]() 的差,若差值的绝对值不超过
的差,若差值的绝对值不超过![]() ,则称所求线性回归方程是“恰当回归方程”.
,则称所求线性回归方程是“恰当回归方程”.
(1)从这![]() 组数据中随机选取
组数据中随机选取![]() 组数据后,求剩下的
组数据后,求剩下的![]() 组数据的间隔时间之差大于
组数据的间隔时间之差大于![]() 的概率;
的概率;
(2)若选取的是后面![]() 组数据,求
组数据,求![]() 关于
关于![]() 的线性回归方程
的线性回归方程![]() ,并判断此方程是否是“恰当回归方程”;
,并判断此方程是否是“恰当回归方程”;
(3)在(2)的条件下,为了使等候的乘客不超过![]() 人,则间隔时间最多可以设置为多少分钟?(精确到整数)
人,则间隔时间最多可以设置为多少分钟?(精确到整数)
参考公式: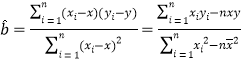 ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在极坐标系中,曲线![]() 的极坐标方程为
的极坐标方程为![]() .现以极点
.现以极点![]() 为原点,极轴为
为原点,极轴为![]() 轴的非负半轴建立平面直角坐标系,直线
轴的非负半轴建立平面直角坐标系,直线![]() 的参数方程为
的参数方程为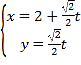 (
(![]() 为参数).
为参数).
(1)求曲线![]() 的直角坐标系方程和直线
的直角坐标系方程和直线![]() 的普通方程;
的普通方程;
(2)点![]() 在曲线
在曲线![]() 上,且到直线
上,且到直线![]() 的距离为
的距离为![]() ,求符合条件的
,求符合条件的![]() 点的直角坐标.
点的直角坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】![]() 年
年![]() 月
月![]() 日,某地援鄂医护人员
日,某地援鄂医护人员![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 人(其中
人(其中![]() 是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这
是队长)圆满完成抗击新冠肺炎疫情任务返回本地,他们受到当地群众与领导的热烈欢迎.当地媒体为了宣传他们的优秀事迹,让这![]() 名医护人员和接见他们的一位领导共
名医护人员和接见他们的一位领导共![]() 人站一排进行拍照,则领导和队长站在两端且
人站一排进行拍照,则领导和队长站在两端且![]() 相邻,而
相邻,而![]() 不相邻的排法种数为( )
不相邻的排法种数为( )
A.![]() 种B.
种B.![]() 种C.
种C.![]() 种D.
种D.![]() 种
种
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以直角坐标系的原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2α﹣4cosα=0.已知直线l的参数方程为![]() (
(![]() 为参数),点M的直角坐标为
为参数),点M的直角坐标为![]() .
.
(1)求直线l和曲线C的普通方程;
(2)设直线l与曲线C交于A,B两点,求![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的四个顶点围成的四边形的面积为
的四个顶点围成的四边形的面积为![]() ,其离心率为
,其离心率为![]()
(1)求椭圆![]() 的方程;
的方程;
(2)过椭圆![]() 的右焦点
的右焦点![]() 作直线
作直线![]() (
(![]() 轴除外)与椭圆
轴除外)与椭圆![]() 交于不同的两点
交于不同的两点![]() ,
,![]() ,在
,在![]() 轴上是否存在定点
轴上是否存在定点![]() ,使
,使![]() 为定值?若存在,求出定点坐标及定值,若不存在,说明理由.
为定值?若存在,求出定点坐标及定值,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com