
【题目】将函数f(x)=2sinx(sinx![]() cosx)﹣1图象向右平移
cosx)﹣1图象向右平移![]() 个单位得函数g(x)的图象,则下列命题中正确的是( )
个单位得函数g(x)的图象,则下列命题中正确的是( )
A.f(x)在(![]() ,
,![]() )上单调递增
)上单调递增
B.函数f(x)的图象关于直线x![]() 对称
对称
C.g(x)=2cos2x
D.函数g(x)的图象关于点(![]() ,0)对称
,0)对称
 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知数集![]() ,其中
,其中![]() ,且
,且![]() ,若对
,若对![]() ,
,![]() 与
与![]() 两数中至少有一个属于
两数中至少有一个属于![]() ,则称数集
,则称数集![]() 具有性质
具有性质![]() .
.
(1)分别判断数集![]() 与数集
与数集![]() 是否具有性质
是否具有性质![]() ,说明理由;
,说明理由;
(2)已知数集![]() 具有性质
具有性质![]() ,判断数列
,判断数列![]() ,
,![]() ,…,
,…,![]() 是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
是否为等差数列,若是等差数列,请证明;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() +
+![]() =1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
=1(a>b>0)的两焦点之间的距离为2,两条准线间的距离为8,直线l:y=k(x-m)(m∈R)与椭圆交于P,Q两点.
(1) 求椭圆C的方程;
(2) 设椭圆的左顶点为A,记直线AP,AQ的斜率分别为k1,k2.①若m=0,求k1k2的值;②若k1k2=-![]() ,求实数m的值.
,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某班级共有50名同学(男女各占一半),为弘扬传统文化,班委组织了“古诗词男女对抗赛”,将同学随机分成25组,每组男女同学各一名,每名同学均回答同样的五个不同问题,答对一题得一分,答错或不答得零分,总分5分为满分.最后25组同学得分如下表:
组别号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 |
男同学得分 | 5 | 4 | 5 | 5 | 4 | 5 | 5 | 4 | 4 | 4 | 5 | 5 | 4 |
女同学得分 | 4 | 3 | 4 | 5 | 5 | 5 | 4 | 5 | 5 | 5 | 5 | 3 | 5 |
分差 | 1 | 1 | 1 | 0 | -1 | 0 | 1 | -1 | -1 | -1 | 0 | 2 | -1 |
组别号 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | |
男同学得分 | 4 | 3 | 4 | 4 | 4 | 4 | 5 | 5 | 5 | 4 | 3 | 3 | |
女同学得分 | 5 | 3 | 4 | 5 | 4 | 3 | 5 | 5 | 3 | 4 | 5 | 5 | |
分差 | -1 | 0 | 0 | -1 | 0 | 1 | 0 | 0 | 2 | 0 | -2 | -2 | |
(I)完成![]() 列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
列联表,并判断是否有90%的把握认为“该次对抗赛是否得满分”与“同学性别”有关;
(Ⅱ)某课题研究小组假设各组男女同学分差服从正态分布![]() ,首先根据前20组男女同学的分差确定
,首先根据前20组男女同学的分差确定![]() 和
和![]() ,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与
,然后根据后面5组同学的分差来检验模型,检验方法是:记后面5组男女同学分差与![]() 的差的绝对值分别为
的差的绝对值分别为![]() ,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在
,若出现下列两种情况之一,则不接受该模型,否则接受该模型.①存在![]() ;②记满足
;②记满足![]() 的i的个数为k,在服从正态分布
的i的个数为k,在服从正态分布![]() 的总体(个体数无穷大)中任意取5个个体,其中落在区间
的总体(个体数无穷大)中任意取5个个体,其中落在区间![]() 内的个体数大于或等于k的概率为P,
内的个体数大于或等于k的概率为P,![]() .
.
试问该课题研究小组是否会接受该模型.
| 0.10 | 0.05 | 0.010 |
| 2.706 | 3.841 | 6.635 |
参考公式和数据: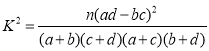
![]() ,
,![]() ;若
;若![]() ,有
,有![]() ,
,![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x2+ax+blnx(a,b∈R),曲线y=f(x)在点(1,f(1))处的切线方程为2x﹣y﹣2=0.
(1)判断f(x)在定义域内的单调性,并说明理由;
(2)若对任意的x∈(1,+∞),不等式f(x)≤m(ex﹣1﹣1)恒成立,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《中国制造2025》是经国务院总理李克强签批,由国务院于2015年5月印发的部署全面推进实施制造强国的战略文件,是中国实施制造强国战略第一个十年的行动纲领.制造业是国民经济的主体,是立国之本、兴国之器、强国之基.发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线.某制造企业根据长期检测结果,发现生产的产品质量与生产标准的质量差都服从正态分布N(μ,σ2),并把质量差在(μ﹣σ,μ+σ)内的产品为优等品,质量差在(μ+σ,μ+2σ)内的产品为一等品,其余范围内的产品作为废品处理.优等品与一等品统称为正品.现分别从该企业生产的正品中随机抽取1000件,测得产品质量差的样本数据统计如下:
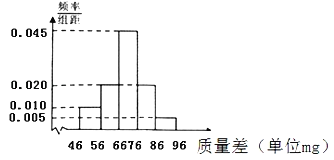
(1)根据频率分布直方图,求样本平均数![]()
(2)根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数![]() 作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
[参考数据:若随机变量ξ服从正态分布N(μ,σ2),则:P(μ﹣σ<ξ≤μ+σ)≈0.6827,P(μ﹣2σ<ξ≤μ+2σ)≈0.9545,P(μ﹣3σ<ξ≤μ+3σ)≈0.9973.
(3)假如企业包装时要求把3件优等品球和5件一等品装在同一个箱子中,质检员每次从箱子中摸出三件产品进行检验,记摸出三件产品中优等品球的件数为X,求X的分布列以及期望值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设数列![]() 的前n项和为
的前n项和为![]() ,
,![]()
(1)求证:数列![]() 是等比数列;
是等比数列;
(2)若![]() ,是否存在q的某些取值,使数列
,是否存在q的某些取值,使数列![]() 中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
中某一项能表示为另外三项之和?若能求出q的全部取值集合,若不能说明理由.
(3)若![]() ,是否存在
,是否存在![]() ,使数列
,使数列![]() 中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
中,某一项可以表示为另外三项之和?若存在指出q的一个取值,若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】很多关于整数规律的猜想都通俗易懂,吸引了大量的数学家和数学爱好者,有些猜想已经被数学家证明,如“费马大定理”,但大多猜想还未被证明,如“哥德巴赫猜想”、“角谷猜想”.“角谷猜想”的内容是:对于每一个正整数,如果它是奇数,则将它乘以![]() 再加1;如果它是偶数,则将它除以
再加1;如果它是偶数,则将它除以![]() ;如此循环,最终都能够得到
;如此循环,最终都能够得到![]() .下图为研究“角谷猜想”的一个程序框图.若输入
.下图为研究“角谷猜想”的一个程序框图.若输入![]() 的值为
的值为![]() ,则输出i的值为( )
,则输出i的值为( )
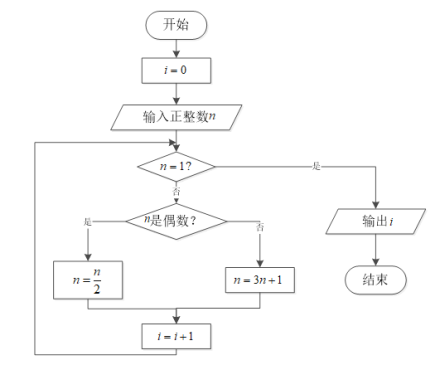
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知椭圆
中,已知椭圆![]() 的左顶点为
的左顶点为![]() ,右焦点为
,右焦点为![]() ,过原点
,过原点![]() 的直线(与坐标轴不重合)与椭圆
的直线(与坐标轴不重合)与椭圆![]() 交于点
交于点![]() 、
、![]() ,直线
,直线![]() 、
、![]() 分别与
分别与![]() 轴交于点
轴交于点![]() 、
、![]() .
.
(1)若![]() ,求点
,求点![]() 的横坐标;
的横坐标;
(2)设直线![]() 、
、![]() 的斜率分别为
的斜率分别为![]() 、
、![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com