
【题目】已知函数![]() .
.
(Ⅰ)设![]() ,讨论
,讨论![]() 的单调性;
的单调性;
(Ⅱ)若对任意![]() 恒有
恒有![]() ,求
,求![]() 的取值范围.
的取值范围.
【答案】(1)当![]() 时,
时,![]()
所以![]() 上为增函数
上为增函数
②当![]() ,由
,由![]()
![]() 上为增函数,
上为增函数,
在![]() 上是减函数
上是减函数
(2)![]()
【解析】
试题(I)![]() 的定义域为(
的定义域为(![]() ,1)
,1)![]() (1,
(1,![]() )
)
![]()
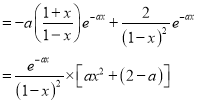
因为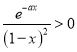 (其中
(其中![]() )恒成立,所以
)恒成立,所以![]()
⑴ 当![]() 时,
时,![]() 在(
在(![]() ,0)
,0)![]() (1,
(1,![]() )上恒成立,所以
)上恒成立,所以![]() 在(
在(![]() ,1)
,1)![]() (1,
(1,![]() )上为增函数;
)上为增函数;
⑵ 当![]() 时,
时,![]() 在(
在(![]() ,0)
,0)![]() (0,1)
(0,1)![]() (1,
(1,![]() )上恒成立,所以
)上恒成立,所以![]() 在(
在(![]() ,1)
,1)![]() (1,
(1,![]() )上为增函数;
)上为增函数;
⑶ 当![]() 时,
时,![]() 的解为:(
的解为:(![]() ,
,![]() )
)![]() (t,1)
(t,1)![]() (1,+
(1,+![]() )
)
(其中![]() )
)
所以![]() 在各区间内的增减性如下表:
在各区间内的增减性如下表:
区间 | ( | ( | (t,1) | (1,+ |
| + |
| + | + |
| 增函数 | 减函数 | 增函数 | 增函数 |
(II)显然![]()
⑴ 当![]() 时,
时,![]() 在区间
在区间![]() 0,1
0,1![]() 上是增函数,所以对任意
上是增函数,所以对任意![]() (0,1)都有
(0,1)都有![]() ;
;
⑵ 当![]() 时,
时,![]() 是
是![]() 在区间
在区间![]() 0,1
0,1![]() 上的最小值,即
上的最小值,即![]() ,这与题目要求矛盾;
,这与题目要求矛盾;
⑶ 若![]() ,
,![]() 在区间
在区间![]() 0,1
0,1![]() 上是增函数,所以对任意
上是增函数,所以对任意![]() (0,1)都有
(0,1)都有![]() 。
。
综合⑴、⑵、⑶ ,a的取值范围为(![]() ,2)
,2)


科目:高中数学 来源: 题型:
【题目】某超市为了解端午节期间粽子的销售量,对其所在销售范围内的1000名消费者在端午节期间的粽子购买量(单位:g)进行了问卷调查,得到如图所示的频率分布直方图.

(Ⅰ)求频率分布直方图中a的值;
(Ⅱ)求这1000名消费者的棕子购买量在600g~1400g的人数;
(Ⅲ)求这1000名消费者的人均粽子购买量(频率分布直方图中同一组的数据用该组区间的中点值作代表).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某超市随机选取![]() 位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
位顾客,记录了他们购买甲、乙、丙、丁四种商品的情况,整理成如下统计表,其中“√”表示购买,“×”表示未购买.
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
(Ⅰ)估计顾客同时购买乙和丙的概率;
(Ⅱ)估计顾客在甲、乙、丙、丁中同时购买![]() 中商品的概率;
中商品的概率;
(Ⅲ)如果顾客购买了甲,则该顾客同时购买乙、丙、丁中那种商品的可能性最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有500名职工,其中不到35岁的有125人,35-49岁的有a人,50岁及以上的有b人,现用分层抽样的方法,从中抽出100名职工了解他们的健康情况:
(1)求不到35岁的职工要抽取的人数;
(2)如果已知35-49岁的职工抽取了56人,求a的值,并求50岁及以上的职工要抽取的人数.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 都是定义域为
都是定义域为![]() 的连续函数.已知:
的连续函数.已知:![]() 满足:①当
满足:①当![]() 时,
时,![]() 恒成立;②
恒成立;②![]() 都有
都有![]() .
.![]() 满足:①
满足:①![]() 都有
都有![]() ;②当
;②当![]() 时,
时,![]() .若关于
.若关于![]() 的不等式
的不等式![]() 对
对![]() 恒成立,则
恒成立,则![]() 的取值范围是
的取值范围是
A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
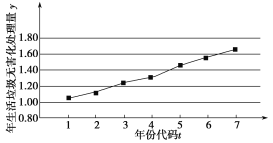
【题目】如图是我国2012年至2018年生活垃圾无害化处理量(单位:亿吨)的折线图.注:年份代码1~7分别对应年份2012~2018.
(1)由折线图看出,可用线性回归模型拟合![]() 与
与![]() 的关系,请用相关系数加以说明;
的关系,请用相关系数加以说明;
(2)建立![]() 关于
关于![]() 的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
的回归方程(系数精确到0.01),预测2020年我国生活垃圾无害化处理量.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式:相关系数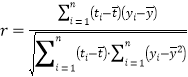 ,回归方程
,回归方程![]() 中斜率和截距的最小二乘估计公式分别为
中斜率和截距的最小二乘估计公式分别为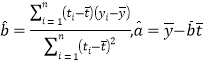 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
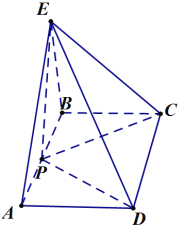
【题目】如图,在矩形ABCD中,AB=2BC,P是线段AB中点,![]() 平面ABCD.
平面ABCD.
(1)求证:![]() 平面EPC;
平面EPC;
(2)问在EP上是否存在点F,使平面![]() 平面BFC?若存在,求出
平面BFC?若存在,求出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com