练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

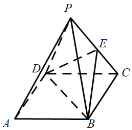
    【题目】如图所示,底面为平行四边形ABCD的四棱锥P-ABCD中,E为PC的中点.求证:PA∥平面BDE.(要求注明每一步推理的大前提、小前提和结论,并最终把推理过程用简略的形式表示出来)

    【答案】见解析

    【解析】

    (1)三角形的中位线与底边平行(大前提),

    连接AC交BD于O,连接OE,由已知OE为△PAC的中位线(小前提),

    所以PA∥OE(结论).

    (2)平面外一条直线和平面内一直线平行,则平面外的直线与该平面平行(大前提),

    PA平面BDE,OE平面BDE(小前提),

    所以PA∥平面BDE(结论).

    上面的证明可简略地写成:

    连接AC交BD于O.连接OE,

    ∵四边形ABCD为平行四边形,

    ∴O为AC的中点.

    又∵E为PC的中点,

    ∴在△PAC中,PA∥OE,OE平面BDE,PA平面BDE,

    ∴PA∥平面BDE.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，直线的参数方程为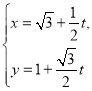（为参数），以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的极坐标方程为.

    （1）求直线的极坐标方程及曲线的直角坐标方程；

    （2）若是直线上一点，是曲线上一点，求的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）时，求的单调区间和最值；

    （2）①若对于任意的，不等式恒成立，求的取值范围；②求证：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】数学老师给出一个函数，甲、乙、丙、丁四个同学各说出了这个函数的一条性质：甲：在 上函数单调递减；乙：在上函数单调递增；丙：在定义域R上函数的图象关于直线对称；丁：不是函数的最小值．老师说：你们四个同学中恰好有三个人说的正确．那么，你认为____说的是错误的．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    (1)若，求曲线在处的切线方程；

    (2)若对任意的，，恒成立，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某大学的名同学准备拼车去旅游，其中大一、大二、大三、大四每个年级各两名，分乘甲、乙两辆汽车.每车限坐名同学(乘同一辆车的名同学不考虑位置)，其中大一的孪生姐妹需乘同一辆车，则乘坐甲车的名同学中恰有名同学是来自于同一年级的乘坐方式共有_______种（有数字作答）.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在直角坐标系中，曲线的方程为.曲线的参数方程为（为参数）.

    (1)求的直角坐标方程；

    (2)若与有三个不同的公共点，求实数的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在含有个元素的集合中，若这个元素的一个排列（，，…，）满足，则称这个排列为集合的一个错位排列（例如：对于集合，排列是的一个错位排列；排列不是的一个错位排列）.记集合的所有错位排列的个数为.

    （1）直接写出，，，的值；

    （2）当时，试用，表示，并说明理由；

    （3）试用数学归纳法证明：为奇数.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知.

    （1）当时，求的单调区间；

    （2）若函数在处取得极大值，求实数a的取值范围.

    查看答案和解析>>

    同步练习册答案