
| A.事件B与事件C互斥 | B.事件A与事件C互斥 |
| C.任两个事件均互斥 | D.任两个事件均不互斥 |
 巧学巧练系列答案
巧学巧练系列答案科目:高中数学 来源:不详 题型:解答题
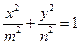
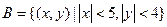 且焦点在X轴的椭圆的概率;
且焦点在X轴的椭圆的概率;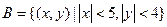 且焦点在X轴的椭圆的情况下,求离心率为
且焦点在X轴的椭圆的情况下,求离心率为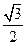
 的概率
的概率查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
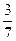 .现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.
.现有甲、乙两人从袋中轮流摸取1球,取后不放回:甲先取,乙后取,然后甲再取……,直到两人中有一人取到白球时即终止.每个球在每一次被取出的机会是等可能的.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| | 高一年级 | 高二年级 | 高三年级 |
| 女生 | 487 | 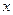 | 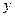 |
| 男生 | 513 | 560 | 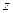 |
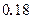 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com