
����Ŀ����ʮ�Ŵ�����ϣ���������ȷǿ������ַ���������ס�����������õ��˸�����������ص�λ�Ļ�����Ӧ.�ڼ��������ż���һ����ѧ�ʵĽڽ�����������У�������ķ���Ҳ�ڲ���������Ϊ����������Ⱥ�ڵĹ�������һ�б���������һ��¥�̿��̼�����Ϊÿƽ�ײ�����7ǧԪ��ÿ��ÿƽ�ļ۸�![]() ��ǧԪ����¥��
��ǧԪ����¥��![]() ֮�����һ�����κ����ı仯���ɣ�����һ����33��ĸ߲�סլ������ۼ�Ϊ�ײ㣨һ¥��ÿƽ��6ǧԪ�����Ϊ��20��ÿƽ��7ǧԪ.
֮�����һ�����κ����ı仯���ɣ�����һ����33��ĸ߲�סլ������ۼ�Ϊ�ײ㣨һ¥��ÿƽ��6ǧԪ�����Ϊ��20��ÿƽ��7ǧԪ.
��1������������Ϣд��������κ����ı���ʽ![]() ��������.
��������.
��2��ij��λ���ǵ�ְ����Ůȥһ�о�ѧ��ʵ����Ҫ���ƻ��Ź�ס����������ȡ�Ź��Ż����ߣ�����õ����Ż���������ÿ���ܼ۵Ļ����ϼ�ȥ20��ǧԪ�����������ľ����۽��������Ϊ95ƽ�ķ��ͳ��۸��õ�λְ������ij����ij�ֱ�ѡ����1¥��25¥��������ݺ������ʣ��Ƚ���ij����ij˭��õ��Żݶ�ȸ���һЩ����һ�ŻݵĶ��Ϊ���٣�ǧԪ������ע��������--��ԭ�۵�![]() ��Ϊ�ּۣ�����ȷ��0.001ǧԪ��.
��Ϊ�ּۣ�����ȷ��0.001ǧԪ��.
���𰸡���1��![]() ��������Ϊ��
��������Ϊ��![]() ����2����ij���Żݶ�ȴ�һЩ��Ϊ51921Ԫ.
����2����ij���Żݶ�ȴ�һЩ��Ϊ51921Ԫ.
��������
��1�����ݶ��κ����趥��ʽ����ʽ������![]() ��⣻
��⣻
��2��д���Żݶ��Ϊ![]() ����ʽ��
����ʽ�� ![]() ��
��![]() ���ֱ������ij����ij���Żݶ�ȼ��ɵý�.
���ֱ������ij����ij���Żݶ�ȼ��ɵý�.
��1������ÿ��ÿƽ�ļ۸�![]() ��ǧԪ����¥��
��ǧԪ����¥��![]() ֮�����һ�����κ����ı仯���ɣ����Ϊ��20��ÿƽ��7ǧԪ��
֮�����һ�����κ����ı仯���ɣ����Ϊ��20��ÿƽ��7ǧԪ��
����![]() ����
����![]() ��
��
����![]() ����ã�
����ã�![]()
����������κ����ı���ʽ![]() ����
����
![]() ����������
����������![]() ��
��
��2�����Żݶ��Ϊ![]() �������Żݷ����ɵã�
�������Żݷ����ɵã�
![]() ��
��![]() ��
��
���ݺ�������ʽ�ɵã�![]() ��һ�����ڳ��µĶ��κ������Գ���
��һ�����ڳ��µĶ��κ������Գ���![]() ��
��
����![]() ��
��
��ij���Żݶ�ȣ�![]()
��ij���Żݶ�ȣ�![]()
������ij���Żݶ�ȴ�һЩ��Ϊ51921Ԫ.


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д� Ŀ�����ϵ�д�
Ŀ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪ij��ѧ�����Ŀư�ѧ������800�˲μ���ѧ�������ѧҵˮƽ���������������ȡ100�˵���ѧ�������ѧҵˮƽ���Գɼ����±���
���� | ��ѧ | |||
���� | ���� | ���� | ||
���� | ���� | 7 | 20 | 5 |
���� | 9 | 18 | 6 | |
���� | a | 4 | b | |
�ɼ���Ϊ���������������������ȼ�������������ֱ��ʾ�����ɼ�����ѧ�ɼ����磺��ʾ��ѧ�ɼ�Ϊ���õĹ���20��18��4��42(��)��
(��)���ڸ�����������ѧ�ɼ�������Ϊ30%����a��b��ֵ��
(��)��֪a��10��b��8��������������������ѧ�ɼ�Ϊ����������ȼ���������ٵĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪![]() Ϊ
Ϊ![]() �������ڽǣ�����
�������ڽǣ�����![]() ������
������![]() ���ߣ��ҽ�
���ߣ��ҽ�![]() Ϊ���.
���.
(1�����![]() �Ĵ�С��
�Ĵ�С��
��2������![]() ��ֵ��.
��ֵ��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ��
��![]() �ĵ���.
�ĵ���.
�������۲���ʽ![]() �Ľ⼯��
�Ľ⼯��
������![]() ��
��![]() ʱ����
ʱ����![]() ��
��![]() ���������
���������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪f(x)��x2��2ax��2(a��R)����x��[��1������)ʱ��![]() ���������a��ȡֵ��Χ��_________��
���������a��ȡֵ��Χ��_________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�ص�ӰԺΪ���˽��Ӱ�ԶԿ�Ҫ��ӳ��һ����Ӱ��Ʊ�۵Ŀ�����������һ�ε��У��õ���Ʊ��x(��λ��Ԫ)�������Ӱ����y(��λ������)�Ľ�����±���
x(��λ��Ԫ) | 30 | 40 | 50 | 60 |
y(�������) | 4.5 | 4 | 3 | 2.5 |
(1)��y��x���н�ǿ����ع�ϵ���Է���y��x֮��������ػ��Ǹ���أ�
(2)������ϱ��ṩ�����ݣ�����С���˷����y����x�����Իع鷽�̣�
(3)����(2)����������Իع鷽�̣�Ԥ��Ʊ�۶�Ϊ����Ԫʱ���ܻ�����Ʊ�����룮
�ο���ʽ��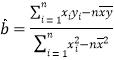 ��
��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����ѧ��50�ˣ�������ͬѧ30�ˣ��÷ֲ�����ķ����Ӹð��ȡ5��ȥ�μ�ij����������
��1����Ӹð���Ůͬѧ�ڸ���ȡ��������
��2���ӳ�ȡ��5��ͬѧ����ѡ2��̸�˻�ĸ��ܣ���ѡ����2��ͬѧ��ǡ��1����ͬѧ�ĸ��ʣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������������⣬P��������ʵ��x����ax2+ax+1��0�������Q������x�ķ���x2��x+a=0��ʵ�����������P��Q��Ϊ�٣�����P��Q��Ϊ�棬��ʵ��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
����![]() ������
������![]() ��ͼ���ڵ�
��ͼ���ڵ�![]() �������߷��̣�
�������߷��̣�
����![]() ʱ������
ʱ������![]() �ĵ�������.
�ĵ�������.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com