
【题目】近几年来,“精准扶贫”是政府的重点工作之一,某地政府对240户贫困家庭给予政府资金扶助,以发展个体经济,提高家庭的生活水平.几年后,一机构对这些贫困家庭进行回访调查,得到政府扶贫资金数、扶贫贫困家庭数![]() (户)与扶贫后脱贫家庭数
(户)与扶贫后脱贫家庭数![]() (户)的数据关系如下:
(户)的数据关系如下:
政府扶贫资金数(万元) | 3 | 5 | 7 | 9 |
政府扶贫贫困家庭数 | 20 | 40 | 80 | 100 |
扶贫后脱贫家庭数 | 10 | 30 | 70 | 90 |
(Ⅰ)求几年来该地依靠“精准扶贫”政策的脱贫率是多少;(答案精准到0.1%)
(Ⅱ)从政府扶贫资金数为3万元和7万元并且扶贫后脱贫的家庭中按分层抽样抽取8户,再从这8户中随机抽取两户家庭,求这两户家庭的政府扶贫资金总和为10万元的概率.
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】(本小题满分16分)
已知数列{an}的前n项和为Sn,且a1=1,Sn=n2an(n∈N*).
(1)试求出S1,S2,S3,S4,并猜想Sn的表达式;
(2)用数学纳法证明你的猜想,并求出an的表达式.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某公司生产某种产品的固定成本为150万元,而每件产品的可变成本为2500元,每件产品的售价为3500元,已知该公司所生产的产品能够全部销售出去.
(1)分别求出总成本![]() (万元),单位成本
(万元),单位成本![]() (万元),销售总收入
(万元),销售总收入![]() (万元),总利润
(万元),总利润![]() (万元)关于总产量x(件)的函数解析式;
(万元)关于总产量x(件)的函数解析式;
(2)由(1)所求得的函数解析式,对这个公司的经济效益作出简单分析.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,曲线C1的参数方程为![]() (
(![]() 为参数),曲线C2的参数方程为
为参数),曲线C2的参数方程为![]() (
(![]() 为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=
为参数).在以O为极点,x轴的正半轴为极轴的极坐标系中,射线l:θ=α 与C1,C2 各有一个交点.当 α=0时,这两个交点间的距离为2,当 α=![]() 时,这两个交点重合.
时,这两个交点重合.
(1) 求曲线C1,C2的直角坐标方程
(2) 设当 α=![]() 时,l与C1,C2的交点分别为A1,B1,当 α=-
时,l与C1,C2的交点分别为A1,B1,当 α=-![]() 时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
时,l与C1,C2的交点分别为A2,B2,求四边形A1A2B2B1的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下命题:
① 双曲线![]() 的渐近线方程为
的渐近线方程为![]() ;
;
② 命题![]() “
“![]() ,
,![]() ”是真命题;
”是真命题;
③ 已知线性回归方程为![]() ,当变量
,当变量![]() 增加
增加![]() 个单位,其预报值平均增加
个单位,其预报值平均增加![]() 个单位;
个单位;
④ 设随机变量![]() 服从正态分布
服从正态分布![]() ,若
,若![]() ,则
,则![]() ;
;
⑤ 已知![]() ,
,![]() ,
,![]() ,
,![]() ,依照以上各式的规律,得到一般性的等式为
,依照以上各式的规律,得到一般性的等式为![]() ,(
,(![]() )
)
则正确命题的序号为 (写出所有正确命题的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,多面体ABCD﹣A1B1C1D1为正方体,则下面结论正确的是( )
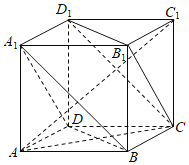
A.A1B∥B1C
B.平面CB1D1⊥平面A1B1C1D1
C.平面CB1D1∥平面A1BD
D.异面直线AD与CB1所成的角为30°
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】我国古代有着辉煌的数学研究成果.《周髀算经》、《九章算术》、《海岛算经》、《孙子算经》、……《缉古算经》等10部专著,有着十分丰富多彩的内容,是了解我国古代数学的重要文献.这10部专著中有7部产生于魏晋南北朝时期.某中学拟从这10部专著中选择2部作为“数学文化”校本课程学习内容,则所选2部专著中至少有一部是魏晋南北朝时期专著的选法为( )
A. 45 种B. 42 种C. 28 种D. 16种
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com