
【题目】设![]() 、
、![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值;
的最大值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() 、
、![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率
的斜率![]() 的取值范围.
的取值范围.
【答案】(1)![]() 的最大值
的最大值![]() ;(2)斜率
;(2)斜率![]() 的取值范围为
的取值范围为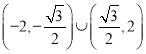
【解析】
(1)设P(x,y),向量坐标化得![]() x2+y2﹣3
x2+y2﹣3![]() .由此能够求出向量乘积
.由此能够求出向量乘积![]() 的取值范围.
的取值范围.
(2)设直线l:y=kx﹣2,M(x1,y1),B(x2,y2),联立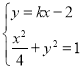 ,得:
,得:![]() ,由韦达定理和根的判别式知:
,由韦达定理和根的判别式知:![]() 或k
或k![]() ,又0°<∠AOB<90°cos∠AOB>0
,又0°<∠AOB<90°cos∠AOB>0![]() 0,由此能求出直线l的斜率k的取值范围.
0,由此能求出直线l的斜率k的取值范围.
(1)根据题意易知![]() ,所以
,所以![]() ,
,
设P(x,y),则
![]() x2+y2﹣3
x2+y2﹣3
![]()
![]() .因为
.因为![]()
故﹣2![]() .
.
(2)显然直线x=0不满足题设条件,
故设直线l:y=kx+2,M(x1,y1),B(x2,y2),
联立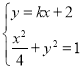 ,消去y,整理得:
,消去y,整理得:![]() ,
,
∴,
由![]() ,
,
得:![]() 或k
或k![]() ,
,
又0°<∠AOB<90°cos∠AOB>0![]() 0,∴x1x2+y1y2>0,
0,∴x1x2+y1y2>0,
又y1y2=(kx1+2)(kx2+2)=k2x1x2+2k(x1+x2)+4

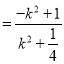 .
.
∵ ,
,
即k2<4,∴﹣2<k<2.
故由①、②得![]() ,或
,或![]() .
.


 作业辅导系列答案
作业辅导系列答案 同步学典一课多练系列答案
同步学典一课多练系列答案科目:高中数学 来源: 题型:
【题目】已知![]() 为坐标原点,
为坐标原点,![]() 为椭圆
为椭圆![]() 的上焦点,
的上焦点,![]() 上一点
上一点![]() 在
在![]() 轴上方,且
轴上方,且![]() .
.
(1)求直线![]() 的方程;
的方程;
(2)![]() 为直线
为直线![]() 与
与![]() 异于
异于![]() 的交点,
的交点,![]() 的弦
的弦![]() ,
,![]() 的中点分别为
的中点分别为![]() ,若
,若![]() 在同一直线上,求
在同一直线上,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】以下四个关于圆锥曲线的命题中
①设A、B为两个定点,k为非零常数,![]() ,则动点P的轨迹为双曲线;
,则动点P的轨迹为双曲线;
②曲线![]() 表示焦点在y轴上的椭圆,则
表示焦点在y轴上的椭圆,则![]() ;
;
③方程2x2-5x+2=0的两根可分别作为椭圆和双曲线的离心率;
④双曲线![]() 与椭圆
与椭圆![]() 有相同的焦点.
有相同的焦点.
其中真命题的序号为______(写出所有真命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
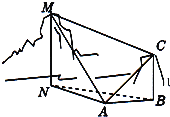
【题目】如图,为测量坡高MN,选择A和另一个山坡的坡顶C为测量观测点.从A点测得M点的仰角∠MAN=60°,C点的仰角∠CAB=45°以及∠MAC=75°;从C点测得∠MCA=60°.已知坡高BC=50米,则坡高MN=______米.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,四棱锥P-ABCD中,AP⊥平面PCD,AD∥BC,AB=BC=![]() AD,E,F分别为线段AD,PC的中点.
AD,E,F分别为线段AD,PC的中点.
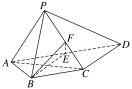
(1)求证:AP∥平面BEF;
(2)求证:BE⊥平面PAC.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】袋子中有四个小球,分别写有“美、丽、中、国”四个字,有放回地从中任取一个小球,直到“中”“国”两个字都取到就停止,用随机模拟的方法估计恰好在第三次停止的概率.利用电脑随机产生0到3之间取整数值的随机数,分别用0,1,2,3代表“中、国、美、丽”这四个字,以每三个随机数为一组,表示取球三次的结果,经随机模拟产生了以下18组随机数:
232 321 230 023 123 021 132 220 001
231 130 133 231 031 320 122 103 233
由此可以估计,恰好第三次就停止的概率为
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某运输公司有![]() 名驾驶员和
名驾驶员和![]() 名工人,有
名工人,有![]() 辆载重量为
辆载重量为![]() 吨的甲型卡车和
吨的甲型卡车和![]() 辆载重量为
辆载重量为![]() 吨的乙型卡车.某天需运往
吨的乙型卡车.某天需运往![]() 地至少
地至少![]() 吨的货物,派用的车需满载且只运送一次.派用的每辆甲型卡车需配
吨的货物,派用的车需满载且只运送一次.派用的每辆甲型卡车需配![]() 名工人,运送一次可得利润
名工人,运送一次可得利润![]() 元:派用的每辆乙型卡车需配
元:派用的每辆乙型卡车需配![]() 名工人,运送一次可得利润
名工人,运送一次可得利润![]() 元,该公司合理计划当天派用两类卡车的车辆数,可得的最大利润多少?
元,该公司合理计划当天派用两类卡车的车辆数,可得的最大利润多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形.谢尔宾斯基三角形是一种分形,由波兰数学家谢尔宾斯基1915年提出.具体操作是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形,如图.

现在上述图(3)中随机选取一个点,则此点取自阴影部分的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥平面ABCD,E为PD的中点.

(1) 证明:PB∥平面AEC
(2) 设二面角D-AE-C为60°,AP=1,AD=![]() ,求三棱锥E-ACD的体积
,求三棱锥E-ACD的体积
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com