
【题目】已知数列![]() ,
,![]() 满足:
满足:![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() ,且
,且![]() .
.
① 记![]() ,求证:数列
,求证:数列![]() 为等差数列;
为等差数列;
② 若数列![]() 中任意一项的值均未在该数列中重复出现无数次,求首项
中任意一项的值均未在该数列中重复出现无数次,求首项![]() 应满足的条件.
应满足的条件.
【答案】(1)![]()
(2)①根据等差数列的定义,证明相邻两项的差为定值来得到证明.从第二项起满足题意即可.
②当![]()
![]() ,数列
,数列![]() 任意一项的值均未在该数列中重复出现无数次
任意一项的值均未在该数列中重复出现无数次
【解析】
试题解:(1)当![]() 时,有
时,有
![]() .
.
又![]() 也满足上式,所以数列
也满足上式,所以数列![]() 的通项公式是
的通项公式是![]() . 4分
. 4分
(2)①因为对任意的![]() ,有
,有![]() ,所以,
,所以,
![]() ,
,
所以,数列![]() 为等差数列. 8分
为等差数列. 8分
②设![]() (其中
(其中![]() 为常数且
为常数且![]() ,
,
所以,![]() ,
,
即数列![]() 均为以7为公差的等差数列. 10分
均为以7为公差的等差数列. 10分
设 .
.
(其中![]() 为
为![]() 中一个常数)
中一个常数)
当![]() 时,对任意的
时,对任意的![]() ,有
,有![]() ; 12分
; 12分
当![]() 时,
时, .
.
(Ⅰ)若![]() ,则对任意的
,则对任意的![]() 有
有![]() ,所以数列
,所以数列![]() 为递减数列;
为递减数列;
(Ⅱ)若![]() ,则对任意的
,则对任意的![]() 有
有![]() ,所以数列
,所以数列![]() 为递增数列.
为递增数列.
综上所述,集合![]() .
.
当![]() 时,数列
时,数列![]() 中必有某数重复出现无数次;
中必有某数重复出现无数次;
当![]() 时,数列
时,数列![]() 均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列
均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列![]() 任意一项的值均未在该数列中重复出现无数次. 18分
任意一项的值均未在该数列中重复出现无数次. 18分


 赢在课堂名师课时计划系列答案
赢在课堂名师课时计划系列答案 天天向上课时同步训练系列答案
天天向上课时同步训练系列答案 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:高中数学 来源: 题型:
【题目】已知直线l的参数方程为: ,(t为参数).在以坐标原点0为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣4ρcosθ﹣4ρsinθ+4=0.
,(t为参数).在以坐标原点0为极点,x轴正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2﹣4ρcosθ﹣4ρsinθ+4=0.
(1)求直线l的普通方程和曲线C的直角坐标方程;
(2)设直线l与曲线C交于A,B两点,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若在定义域内存在
,若在定义域内存在![]() ,使得
,使得![]() 成立,则称
成立,则称![]() 为函数
为函数![]() 的局部对称点.
的局部对称点.
(1)若![]() 、
、![]() 且
且![]() ,证明:函数
,证明:函数![]() 必有局部对称点;
必有局部对称点;
(2)若函数![]() 在区间
在区间![]() 内有局部对称点,求实数
内有局部对称点,求实数![]() 的取值范围;
的取值范围;
(3)若函数![]() 在
在![]() 上有局部对称点,求实数
上有局部对称点,求实数![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】部分与整体以某种相似的方式呈现称为分形,一个数学意义上分形的生成是基于一个不断迭代的方程式,即一种基于递归的反馈系统.分形几何学不仅让人们感悟到科学与艺木的融合,数学与艺术审美的统一,而且还有其深刻的科学方法论意义.如图,由波兰数学家谢尔宾斯基1915年提出的谢尔宾斯基三角形就属于-种分形,具体作法是取一个实心三角形,沿三角形的三边中点连线,将它分成4个小三角形,去掉中间的那一个小三角形后,对其余3个小三角形重复上述过程逐次得到各个图形.

若在图④中随机选取-点,则此点取自阴影部分的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四边形ABCD为正方形,PD⊥平面ABCD,PD∥QA,QA=AB=![]() PD.
PD.

(I)证明:平面PQC⊥平面DCQ
(II)求二面角Q-BP-C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电器专卖店销售某种型号的空调,记第![]() 天(
天(![]() ,
,![]() )的日销售量为
)的日销售量为![]() (单位;台).函数
(单位;台).函数![]() 图象中的点分别在两条直线上,如图,该两直线交点的横坐标为
图象中的点分别在两条直线上,如图,该两直线交点的横坐标为![]() ,已知
,已知![]() 时,函数
时,函数![]() .
.

(1)当![]() 时,求函数
时,求函数![]() 的解析式;
的解析式;
(2)求![]() 的值及该店前
的值及该店前![]() 天此型号空调的销售总量;
天此型号空调的销售总量;
(3)按照经验判断,当该店此型号空调的销售总量达到或超过![]() 台,且日销售量仍持续增加时,该型号空调开始旺销,问该店此型号空调销售到第几天时,才可被认为开始旺销?
台,且日销售量仍持续增加时,该型号空调开始旺销,问该店此型号空调销售到第几天时,才可被认为开始旺销?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知首项大于0的等差数列![]() 的公差
的公差![]() ,且
,且![]() ;
;
(1)求数列![]() 的通项公式;
的通项公式;
(2)若数列![]() 满足:
满足:![]() ,
,![]() ,
,![]() ,其中
,其中![]() ;
;
①求数列![]() 的通项
的通项![]() ;
;
②是否存在实数![]() ,使得数列
,使得数列![]() 为等比数列?若存在,求出
为等比数列?若存在,求出![]() 的值,若不存在,请说明理由;
的值,若不存在,请说明理由;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为![]() (其中
(其中![]() 为参数),曲线
为参数),曲线![]() 的参数方程为
的参数方程为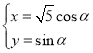 (其中
(其中![]() 为参数),以原点
为参数),以原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)求曲线![]() 、
、![]() 的极坐标方程;
的极坐标方程;
(2)射线![]() :
:![]() 与曲线
与曲线![]() ,
,![]() 分别交于点
分别交于点![]() ,
,![]() (且点
(且点![]() ,
,![]() 均异于原点
均异于原点![]() ),当
),当![]() 时,求
时,求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 、
、![]() 、
、![]() 、
、![]() (
(![]() ),都在函数
),都在函数![]() (
(![]() ,
,![]() )的图像上;
)的图像上;
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等比数列;
是等比数列;
(2)设![]() ,函数
,函数![]() 的反函数为
的反函数为![]() ,若函数
,若函数![]() 与函数
与函数![]() 的图像有公共点
的图像有公共点![]() ,求证:
,求证:![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,
,![]() (
(![]() ),过点
),过点![]() 、
、![]() 的直线
的直线![]() 与两坐标轴围成的三角形面积为
与两坐标轴围成的三角形面积为![]() ,问:数列
,问:数列![]() 是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
是否存在最大项?若存在,求出最大项的值,若不存在,请说明理由;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com