定义在R上的函数y=f(x)是增函数,且函数y=f(x-2)的图象关于(2,0)成中心对称,若s,t满足不等式f(s2-4s)≥-f(4t-t2),若-2≤s≤2时,则3t+s的最大值为 .
【答案】
分析:根据函数图象平移的公式结合奇偶性定义,可得函数y=f(x)是奇函数.因此将f(s
2-4s)≥-f(4t-t
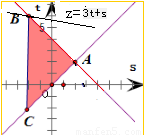
2)变形,化简整理得到(s-t)(s+t-4)≥0,以s为横坐标、t为纵坐标建立坐标系,结合-2≤s≤2作出不等式组表示的平面区域如图所示.再将z=3t+s对应的直线l进行平移,即可得到当s=-2,t=6时,3t+s的最大值为16.
解答:解:∵y=f(x-2)的图象由y=f(x)函数图象向右移2个单位而得
∴由y=f(x-2)图象关于(2,0)点对称,可得函数y=f(x)的图象关于(0,0)点对称.
由此可得函数y=f(x)是奇函数
∴f(4t-t
2)=-f(t
2-4t)
∵f(s
2-4s)≥-f(4t-t
2),∴f(s
2-4s)≥f(t
2-4t)
又∵y=f(x)函数是增函数,
∴s
2-4s≥t
2-4t,移项得:s
2-4s-t
2+4t≥0
化简整理可得:(s-t)(s+t-4)≥0
以s为横坐标、t为纵坐标,建立如图直角坐标系,
则不等式
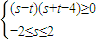
表示的平面区域如图所示
即△ABC及其内部,其中A(2,2),B(-2,6),C(-2,-2)
设z=F(s,t)=3t+s,将直线l:z=3t+s进行平移,
可得当l经过点B时,z达到最大值
∴z
max=F(s,t)=3×6+(-2)=16
故答案为:16
点评:本题以函数的奇偶性和不等式等价变形为载体,考查了函数的图象与基本性质、二元一次不等式表示的平面区域和简单的线性规划等知识,属于中档题.


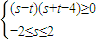 表示的平面区域如图所示
表示的平面区域如图所示
