
【题目】某校从高一年级学生中随机抽取60名学生,将期中考试的物理成绩(均为整数)分成六段:![]() ,
,![]() ,
,![]() ,…,
,…,![]() 后得到如图频率分布直方图.
后得到如图频率分布直方图.
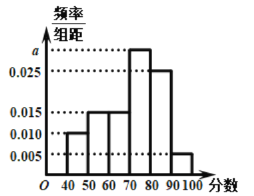
(1)根据频率分布直方图,估计众数和中位数;
(2)用分层抽样的方法从![]() 的学生中抽取一个容量为5的样本,从这五人中任选两人参加补考,求这两人的分数至少一人落在
的学生中抽取一个容量为5的样本,从这五人中任选两人参加补考,求这两人的分数至少一人落在![]() 的概率.
的概率.
【答案】(1)众数为75,中位数为73.33;(2)![]() .
.
【解析】
(1)由频率分布直方图能求出a=0.030.由此能求出众数和中位数;(2)用分层抽样的方法从[40,60)的学生中抽取一个容量为5的样本,从这五人中任选两人参加补考,基本事件总数![]() ,这两人的分数至少一人落在[50,60)包含的基本事件个数
,这两人的分数至少一人落在[50,60)包含的基本事件个数![]() ,由此能求出这两人的分数至少一人落在[50,60)的概率.
,由此能求出这两人的分数至少一人落在[50,60)的概率.
(1)由频率分布直方图得:
![]() ,
,
解得![]() ,
,
所以众数为:![]() ,
,
![]() 的频率为
的频率为![]() ,
,![]() 的频率为
的频率为![]() ,
,
中位数为:![]() .
.
(2)用分层抽样的方法从![]() 的学生中抽取一个容量为5的样本,
的学生中抽取一个容量为5的样本,![]() 的频率为0.1,
的频率为0.1,![]() 的频率为0.15,
的频率为0.15,![]() 中抽到
中抽到![]() 人,
人,![]() 中抽取
中抽取![]() 人,
人,
从这五人中任选两人参加补考,
基本事件总数![]() ,
,
这两人的分数至少一人落在![]() 包含的基本事件个数
包含的基本事件个数![]() ,
,
所以这两人的分数至少一人落在![]() 的概率
的概率![]() .
.


 智能训练练测考系列答案
智能训练练测考系列答案科目:高中数学 来源: 题型:
【题目】某车间在两天内,每天生产10件某产品,其中第一天第二天分别生产了1件2件次品,而质检部每天要在生产的10件产品中随意抽取4件进行检查,若发现有次品,则当天的产品不能通过.
(1)求两天全部通过检查的概率;
(2)若厂内对该车间生产的产品质量采用奖惩制度,两天全不通过检查罚300元,通过1天,2天分别奖300元900元.那么该车间在这两天内得到奖金的数学期望是多少元?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,若给定非零实数
,若给定非零实数![]() ,对于任意实数
,对于任意实数![]() ,总存在非零常数
,总存在非零常数![]() ,使得
,使得![]() 恒成立,则称函数
恒成立,则称函数![]() 是
是![]() 上的
上的![]() 级
级![]() 类周期函数,若函数
类周期函数,若函数![]() 是
是![]() 上的2级2类周期函数,且当
上的2级2类周期函数,且当![]() 时,
时,![]() ,又函数
,又函数![]() .若
.若![]() ,
,![]() ,使
,使![]() 成立,则实数
成立,则实数![]() 的取值范围是_______.
的取值范围是_______.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】学校艺术节对![]() 四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
四件参赛作品只评一件一等奖,在评奖揭晓前,甲,乙,丙,丁四位同学对这四件参赛作品预测如下:
甲说:“是![]() 或
或![]() 作品获得一等奖”; 乙说:“
作品获得一等奖”; 乙说:“ ![]() 作品获得一等奖”;
作品获得一等奖”;
丙说:“ ![]() 两件作品未获得一等奖”; 丁说:“是
两件作品未获得一等奖”; 丁说:“是![]() 作品获得一等奖”.
作品获得一等奖”.
评奖揭晓后,发现这四位同学中只有两位说的话是对的,则获得一等奖的作品是_________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】点![]() 是抛物线
是抛物线![]() :
:![]() 的焦点,动直线
的焦点,动直线![]() 过点
过点![]() 且与抛物线
且与抛物线![]() 相交于
相交于![]() ,
,![]() 两点.当直线
两点.当直线![]() 变化时,
变化时,![]() 的最小值为4.
的最小值为4.
(1)求抛物线![]() 的标准方程;
的标准方程;
(2)过点![]() ,
,![]() 分别作抛物线
分别作抛物线![]() 的切线
的切线![]() ,
,![]() ,
,![]() 与
与![]() 相交于点
相交于点![]() ,
,![]() ,
,![]() 与
与![]() 轴分别交于点
轴分别交于点![]() ,
,![]() ,求证:
,求证:![]() 与
与![]() 的面积之比为定值(
的面积之比为定值(![]() 为坐标原点).
为坐标原点).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,设P、M、N分别是正方体的棱![]() ,AD,AB上非顶点的任意点.
,AD,AB上非顶点的任意点.
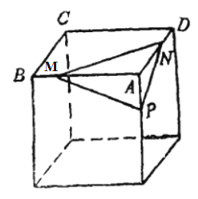
①![]() 的外心必在
的外心必在![]() 的某一边上;
的某一边上;
②![]() 的外心必在
的外心必在![]() 的内部;
的内部;
③![]() 的垂心必是点A在平面PMN上的射影;
的垂心必是点A在平面PMN上的射影;
④若线段AP、AM、AN的长分别为a、b、c,则![]() .其中( ).
.其中( ).
A. 只有①、④正确.
B. 只有③、④正确.
C. 只有②、③、④正确.
D. 只有②、③正确.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为椭圆
分别为椭圆![]() 的左、右焦点,点
的左、右焦点,点![]() 在椭圆上,且
在椭圆上,且![]() 轴,
轴,![]() 的周长为6.
的周长为6.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过点![]() 的直线与椭圆
的直线与椭圆![]() 交于
交于![]() ,
,![]() 两点,设
两点,设![]() 为坐标原点,是否存在常数
为坐标原点,是否存在常数![]() ,使得
,使得![]() 恒成立?请说明理由.
恒成立?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com