
| A. | $[\frac{1}{4},1)$ | B. | $(0,\frac{1}{4}]$ | C. | $[\frac{3}{4},1)$ | D. | $(0,\frac{3}{4}]$ |
分析 两个函数的恒成立问题转化为最值问题,此题4x-logax≤$\frac{3}{2}$对x∈(0,$\frac{1}{2}$)恒成立,函数$y={4^x}-\frac{3}{2}$的图象不在y=logax图象的上方.对数函数另一方面要注意分类对底数a讨论.即可求解
解答  解:由题意得${4^x}-\frac{3}{2}≤{log_a}x$在$x∈(0,\frac{1}{2}]$上恒成立,
解:由题意得${4^x}-\frac{3}{2}≤{log_a}x$在$x∈(0,\frac{1}{2}]$上恒成立,
即当$x∈(0,\frac{1}{2}]$时,函数$y={4^x}-\frac{3}{2}$的图象不在y=logax图象的上方,
由图知:当a>1时,函数$y={4^x}-\frac{3}{2}({0<x≤\frac{1}{2}})$的图象在y=logax图象的上方;
当0<a<1时,${log_a}\frac{1}{2}≥\frac{1}{2}$,解得$\frac{1}{4}≤a<1$.
故选:A.
点评 本题考查了函数在其定义域内值域的问题,两个函数的恒成立问题转化为最值问题.对数函数另一方面要注意分类对底数a讨论.属于中档题.


科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 1 | C. | $\frac{1}{16}$ | D. | $\frac{1}{32}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
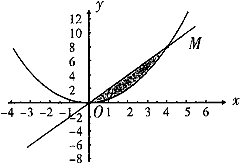 设曲线x2=2y与过原点的直线相交于点M,若直线OM的倾斜角为θ,则线段OM与曲线围成的封闭图形的面积S(θ)的图象大致是( )
设曲线x2=2y与过原点的直线相交于点M,若直线OM的倾斜角为θ,则线段OM与曲线围成的封闭图形的面积S(θ)的图象大致是( )| A. | 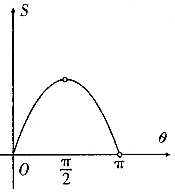 | B. | 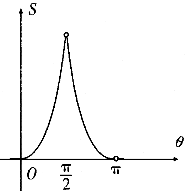 | ||
| C. | 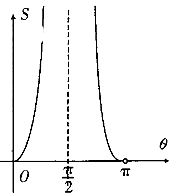 | D. | 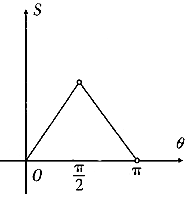 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com