
【题目】已知椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() ,长轴长为4,离心率为
,长轴长为4,离心率为![]() .过右焦点
.过右焦点![]() 的直线
的直线![]() 交椭圆
交椭圆![]() 于
于![]() 两点(均不与
两点(均不与![]() 重合),记直线
重合),记直线![]()
![]() 的斜率分别为
的斜率分别为![]() .
.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)是否存在常数![]() ,当直线
,当直线![]() 变动时,总有
变动时,总有![]() 成立?若存在,求出
成立?若存在,求出![]() 的值;若不存在,说明理由.
的值;若不存在,说明理由.
科目:高中数学 来源: 题型:
【题目】已知a>0,且a≠1.命题P:函数f(x)=logax在(0,+∞)上为增函数;命题Q:函数g(x)=x2﹣2ax+4有零点.
(1)若命题P,Q满足P真Q假,求实数a的取值范围;
(2)命题S:函数y=f(g(x))在区间[2,+∞)上值恒为正数.若命题S为真命题,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,直角梯形ABCD中,AB∥CD,∠BAD=90°,AB=AD=1,CD=2,若将△BCD沿着BD折起至△BC'D,使得AD⊥BC'.

(1)求证:平面C'BD⊥平面ABD;
(2)求C'D与平面ABC'所成角的正弦值;
(3)M为BD中点,求二面角M﹣AC'﹣B的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() =2cos(ωx
=2cos(ωx![]() )(ω>0)满足:f(
)(ω>0)满足:f(![]() )=f(
)=f(![]() ),且在区间(
),且在区间(![]() ,
,![]() )内有最大值但没有最小值,给出下列四个命题:P1:
)内有最大值但没有最小值,给出下列四个命题:P1:![]() 在[0,2π]上单调递减;P2:
在[0,2π]上单调递减;P2:![]() 的最小正周期是4π;P3:
的最小正周期是4π;P3:![]() 的图象关于直线x
的图象关于直线x![]() 对称;P4:
对称;P4:![]() 的图象关于点(
的图象关于点(![]() ,0)对称.其中的真命题是( )
,0)对称.其中的真命题是( )
A.P1,P2B.P2,P4C.P1,P3D.P3,P4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校组织高一、高二年级学生进行了“纪念建国70周年”的知识竞赛.从这两个年级各随机抽取了40名学生,对其成绩进行分析,得到了高一年级成绩的频率分布直方图和高二年级成绩的频数分布表.
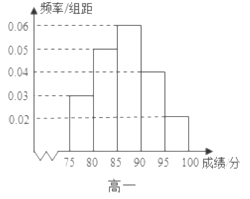
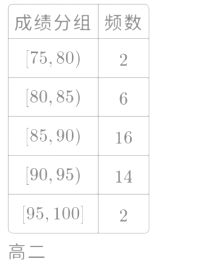
(Ⅰ)若成绩不低于80分为“达标”,估计高一年级知识竞赛的达标率;
(Ⅱ)在抽取的学生中,从成绩为[95,100]的学生中随机选取2名学生,代表学校外出参加比赛,求这2名学生来自于同一年级的概率;
(Ⅲ)记高一、高二两个年级知识竞赛的平均分分别为![]() ,试估计
,试估计![]() 的大小关系.(只需写出结论)
的大小关系.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线E的极坐标方程为4(ρ2-4)sin2θ=(16-ρ2)cos2θ,以极轴为x轴的非负半轴,极点O为坐标原点,建立平面直角坐标系.
(1)写出曲线E的直角坐标方程;
(2)若点P为曲线E上动点,点M为线段OP的中点,直线l的参数方程为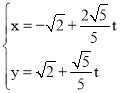 (t为参数),求点M到直线l的距离的最大值.
(t为参数),求点M到直线l的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() ,
,![]() 分别为双曲线
分别为双曲线![]()
![]()
![]() 的左、右焦点,点P是以
的左、右焦点,点P是以![]() 为直径的圆与C在第一象限内的交点,若线段
为直径的圆与C在第一象限内的交点,若线段![]() 的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
的中点Q在C的渐近线上,则C的两条渐近线方程为__________.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某商场从2018年1月份起的前这个月,顾客对某商品的需求总量,![]() (单位:件)与x的关系近似地满足
(单位:件)与x的关系近似地满足![]() (其中
(其中![]() ,且
,且![]() ),该商品第x月的进货单价
),该商品第x月的进货单价![]() (单位:元)与x的近似关系是
(单位:元)与x的近似关系是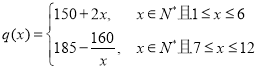 .
.
(1)写出2018年第x月的需求量![]() (单位:件)与x的函数关系式;
(单位:件)与x的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,试问该商场2018年第几个月销售该商品的月利润![]() 最大,最大月利润为多少元?
最大,最大月利润为多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com