
分析 ①若AB是斜边,则根据题中二面角的大小,首先要作出此二面角的平面角,可以取AB中点M,连接MC1、MC2,则∠C1MC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,进而可以求得答案;
②若AB是直角边,则∠C1AC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,进一步可得答案;
③如图3所示:AB为公共直角边时,C1在靠近A的这侧,但是C2在靠近B的那侧.
解答 解:①如图1所示:当AB为斜边时,取AB中点M,连接MC1、MC2,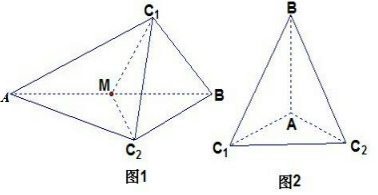
∵△ABC1和△ABC2均为等腰直角三角形,
∴MC1⊥AB,MC2⊥AB,则∠C1MC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,
∴∠C1MC2=60°,
又∵MC1=MC2=$\frac{\sqrt{2}}{2}$,
∴C1C2=$\frac{\sqrt{2}}{2}$;
②如图2所示:当AB为直角边时,
∵BA⊥AC1,BA⊥AC2,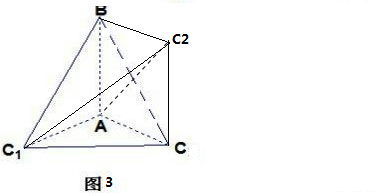
∴∠C1AC2即为等腰直角△ABC1和△ABC2所在的平面构成的二面角的平面角,
∴∠C1AC2=60°,
又∵C1A=C2A=1,
∴C1C2=1;
③如图3所示:AB为公共直角边时,C1在靠近A的这侧,但是C2在靠近B的那侧,
此时C1C2=$\sqrt{2}$,
综上所述:点C1和C2之间的距离等于$\frac{\sqrt{2}}{2}$或1或$\sqrt{2}$.
故答案为:$\sqrt{2},1,\frac{{\sqrt{2}}}{2}$.
点评 本题主要考查点、线、面之间的距离计算,二面角及其度量等基本知识,同时考查空间想象能力和推理、运算能力,是中档题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{a+b}{b}$=$\frac{c+d}{c}$ | B. | $\frac{a+c}{c}$=$\frac{b+d}{d}$ | C. | $\frac{a-c}{c}$=$\frac{b-d}{b}$ | D. | $\frac{a-c}{a}$=$\frac{b-d}{d}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{3}$ | B. | $\frac{π}{2}$ | C. | $\frac{2π}{3}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,+∞) | B. | (-∞,1) | C. | (-1,1) | D. | (-∞,-1)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
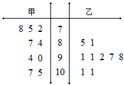 某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )
某次运动会甲、乙两名射击运动员成绩如图所示,甲、乙的平均数分别为为 $\overline{{x}_{甲}}$、$\overline{{x}_{乙}}$,方差分别为s甲2,s乙2,则( )| A. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2>s乙2 | B. | $\overline{{x}_{甲}}$>$\overline{{x}_{乙}}$,s甲2<s乙2 | ||
| C. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2>s乙2 | D. | $\overline{{x}_{甲}}$<$\overline{{x}_{乙}}$,s甲2<s乙2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $f(\frac{3}{4})<f({a^2}-a+1)$ | B. | $f(\frac{3}{4})≤f({a^2}-a+1)$ | C. | $f(\frac{3}{4})>f({a^2}-a+1)$ | D. | $f(\frac{3}{4})≥f({a^2}-a+1)$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com