
如图所示,平面
 平面
平面 ,且四边形
,且四边形 为矩形,四边形
为矩形,四边形 为直角梯形,
为直角梯形, ,
, ,
, ,
, .
.
(1)求证
 平面
平面 ;(2)求平面
;(2)求平面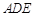 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
(1)证明见解析;(2)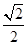 .
.
解析试题分析:(方法一:传统几何方法)(1)证明线面平行,可在平面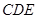 内找到一条线与面外的线AF平行即可,因此本小题可取CE中点为G,连接DG,FG,证明四边形AFGD为平行四边形即可完成证明;(2)本小题中可过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,把问题转化为证明
内找到一条线与面外的线AF平行即可,因此本小题可取CE中点为G,连接DG,FG,证明四边形AFGD为平行四边形即可完成证明;(2)本小题中可过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,把问题转化为证明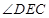 为平面
为平面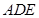 与平面
与平面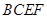 所成锐二面角的平面角,再利用直角三角形的边角关系算出其余弦值.
所成锐二面角的平面角,再利用直角三角形的边角关系算出其余弦值.
(方法二:空间向量方法)(1)本小题可以以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立空间直角坐标系,把问题转化为证明AF的方向向量与平面CDE的一个法向量垂直(证它们的数量积为零),而根据题意易得这个法向量为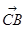 ;(2)本小题为常考的利用空间向量解决面面角问题,只需找到这两个面的法向量
;(2)本小题为常考的利用空间向量解决面面角问题,只需找到这两个面的法向量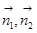 ,利用公式
,利用公式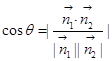 完成计算即可,但要注意本题面面角为锐二面角.
完成计算即可,但要注意本题面面角为锐二面角.
试题解析:(方法一:)(1)取CE中点为G,连接DG,FG,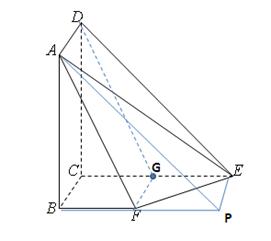
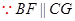 且
且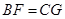 ,∴四边形BFGC为平行四边形,则
,∴四边形BFGC为平行四边形,则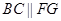 且
且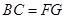 .
.
∵四边形ABCD为矩形,∴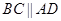 且
且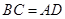 ,∴
,∴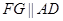 且
且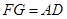 ,
,
∴四边形AFGD为平行四边形,则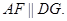
∵ ,
, ,∴
,∴ .
.
(2)过点E作CB的平行线交BF的延长线于P,连接FP,EP,AP,
∵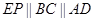 ,∴A,P,E,D四点共面.
,∴A,P,E,D四点共面. 四边形
四边形 为直角梯形,四边形
为直角梯形,四边形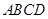 为矩形,
为矩形,
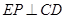 ,
,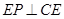 ,又
,又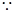
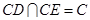 ,
,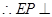 平面
平面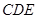 ,
,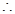
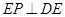 ,又
,又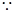 平面
平面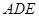
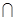 平面
平面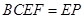 ,
,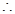
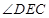 为平面
为平面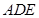 与平面
与平面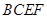 所成锐二面角的平面角.
所成锐二面角的平面角.
 ,
,
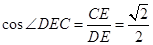 .即平面
.即平面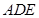 与平面
与平面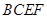 所成锐二面角的余弦值为
所成锐二面角的余弦值为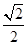 .
.
(方法二:)(1)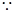 四边形
四边形 为直角梯形,四边形
为直角梯形,四边形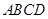 为矩形,
为矩形,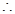
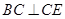 ,
,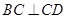 ,又
,又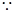 平面
平面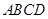
 平面
平面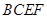 ,且平面
,且平面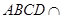 平面
平面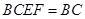 ,∴
,∴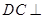 平面
平面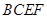 ,以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立如图所示空间直角坐标系.
,以C为原点,CB所在直线为x轴,CE所在直线为y轴,CD所在直线为z轴建立如图所示空间直角坐标系.

 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:解答题
如图,点 为斜三棱柱
为斜三棱柱 的侧棱
的侧棱 上一点,
上一点,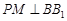 交
交 于点
于点 ,
, 交
交 于点
于点 .
.
(1) 求证: ;
;
(2) 在任意 中有余弦定理:
中有余弦定理: .
.
拓展到空间,类比三角形的余弦定理,写出斜三棱柱的三个侧面面积与其中两个侧面所成的二面角之间的关系式,并予以证明
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在直三棱柱中 -A BC中,AB
-A BC中,AB 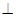 AC, AB=AC=2,
AC, AB=AC=2,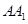 =4,点D是BC的中点.
=4,点D是BC的中点.
(1)求异面直线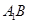 与
与 所成角的余弦值;
所成角的余弦值;
(2)求平面 与
与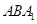 所成二面角的正弦值.
所成二面角的正弦值.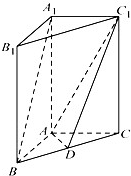
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图. 直三棱柱ABC —A1B1C1中,A1B1= A1C1,点D、E分别是棱BC,CC1上的点(点D不同于点C),且AD⊥DE,F为B1C1的中点.
求证:(1)平面ADE⊥平面BCC1B1
(2)直线A1F∥平面ADE.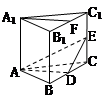
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com