
【题目】在等差数列{an}中,a1=2,a3+a5=16. (Ⅰ)求数列{an}的通项公式;
(Ⅱ)如果a2 , am , a2m成等比数列,求正整数m的值.
【答案】解:(Ⅰ)设等差数列{an}的公差为d,
则a3+a5=2a1+6d=16,
又因为a1=2,
解得d=2.
所以an=a1+(n﹣1)d=2n;
(Ⅱ)因为a2,am,a2m成等比数列,
所以 ![]() ,
,
即(2m)2=4×4m,m∈N*,
解得m=4.
【解析】(Ⅰ)设等差数列{an}的公差为d,结合题意可得a3+a5=2a1+6d=16,解可得d的值,代入等差数列的通项公式即可得答案;(Ⅱ)根据题意,由等比数列的性质可得 ![]() ,结合等差数列的通项公式可得(2m)2=4×4m,解可得m的值,即可得答案.
,结合等差数列的通项公式可得(2m)2=4×4m,解可得m的值,即可得答案.
【考点精析】本题主要考查了等差数列的通项公式(及其变式)和等比数列的通项公式(及其变式)的相关知识点,需要掌握通项公式:![]() 或
或![]() ;通项公式:
;通项公式:![]() 才能正确解答此题.
才能正确解答此题.


 提分百分百检测卷系列答案
提分百分百检测卷系列答案科目:高中数学 来源: 题型:
【题目】某科技研究所对一批新研发的产品长度进行检测(单位:mm),如图是检测结果的频率分布直方图,据此估计这批产品的中位数为( ) 
A.20
B.22.5
C.22.75
D.25
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2014年“五一节”期间,高速公路车辆较多,交警部门通过路面监控装置抽样调查某一山区路段汽车行驶速度,采用的方法是:按到达监控点先后顺序,每隔50辆抽取一辆,总共抽取120辆,分别记下其行车速度,将行车速度(km/h)分成七段[60,65),[65,70),[70,75),[75,80),[80,85),[85,90),[90,95)后得到如图所示的频率分布直方图,据图解答下列问题: 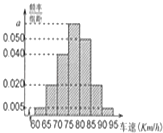
(1)求a的值,并说明交警部门采用的是什么抽样方法?
(2)求这120辆车行驶速度的众数和中位数的估计值(精确到0.1);
(3)若该路段的车速达到或超过90km/h即视为超速行驶,试根据样本估计该路段车辆超速行驶的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设OABC是四面体,G1是△ABC的重心,G是OG1上一点,且OG=3GG1 , 若 ![]() =x
=x ![]() +y
+y ![]() +z
+z ![]() ,则(x,y,z)为( )
,则(x,y,z)为( )
A.( ![]() ,
, ![]() ,
, ![]() )
)
B.( ![]() ,
, ![]() ,
, ![]() )
)
C.( ![]() ,
, ![]() ,
, ![]() )
)
D.( ![]() ,
, ![]() ,
, ![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位用2160万元购得一块空地,计划在该地块上建造一栋至少10层,每层2000平方米的楼房.经测算,如果将楼房建为x(x≥10)层,则每平方米的平均建筑费用为560+48x(单位:元).
(注:平均综合费用=平均建筑费用+平均购地费用,平均购地费用= ![]() )
)
(1)写出楼房平均综合费用y关于建造层数x的函数关系式;
(2)该楼房应建造多少层时,可使楼房每平方米的平均综合费用最少?最少值是多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列{an}的前n项和为Sn , 且a1=1,当n≥2时,Sn=2an .
(1)求证数列{an}为等比数列,并求出an的通项公式;
(2)设若bn=an+1﹣1,设数列{anbn}的前n项和为Tn , 求Tn .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F1 , F2是椭圆 ![]() (a>b>0)的两个焦点,O为坐标原点,点P(﹣1,
(a>b>0)的两个焦点,O为坐标原点,点P(﹣1, ![]() )在椭圆上,且
)在椭圆上,且 ![]()
![]() =0,⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B
=0,⊙O是以F1F2为直径的圆,直线l:y=kx+m与⊙O相切,并且与椭圆交于不同的两点A,B
(1)求椭圆的标准方程;
(2)当 ![]()
![]() =λ,且满足
=λ,且满足 ![]() ≤λ≤
≤λ≤ ![]() 时,求弦长|AB|的取值范围.
时,求弦长|AB|的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com