
| A. | [-1,2] | B. | [-1,4] | C. | [$\frac{1}{2}$,4] | D. | [$\frac{1}{2}$,2] |
 全能测控期末小状元系列答案
全能测控期末小状元系列答案 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案科目:高中数学 来源:2016-2017学年湖南益阳市高二9月月考数学(理)试卷(解析版) 题型:解答题
如图,在四棱锥P﹣ABCD中,底面ABCD为菱形,∠BAD=60°,Q为AD的中点.
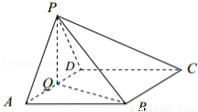
(1)若PA=PD,求证:平面PQB⊥平面PAD;
(2)若平面PAD⊥平面ABCD,且PA=PD=AD=2,点M在线段PC上,且PM=3MC,求三棱锥P﹣QBM的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
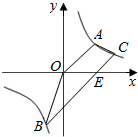 如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.
如图,梯形AOBC的顶点A,C在反比例函数图象上,OA∥BC,上底边OA在直线y=x上,下底边BC交x轴于E(2,0),C点的纵坐标为1.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
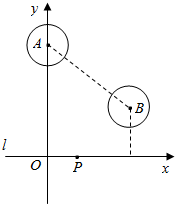 如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).
如图l是东西走向的一水管,在水管北侧有两个半径都是10m的圆形蓄水池A,B(A,B分别为蓄水池的圆心),经测量,点A,B到水管l的距离分别为55m和25m,AB=50m.以l所在直线为x轴,过点A且与l垂直的直线为y轴,建立如图所示的直角坐标系(O为坐标原点).查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 4 | B. | -4 | C. | $\frac{1}{4}$ | D. | -$\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com