Question

已知正方体ABCD-A₁B₁C₁D₁，求：
（1）异面直线AD₁与A₁B所成的角；
（2）证明：直线A₁B∥平面AD₁C
（3）二面角D-A₁B-C₁的大小．

Answer 1

考点：二面角的平面角及求法,直线与平面平行的判定

专题：空间位置关系与距离,空间角

分析：（1）连结D₁C，AC，则A₁B∥D₁C，从而异面直线AD₁与A₁B所成的角为∠AD₁C，由△AD₁C是等边三角形，能求出异面直线AD₁与A₁B所成的角的大小．
（2）由A₁B∥D₁C，能证明直线A₁B∥平面AD₁C．
（3）以D为原点，建立空间直角坐标系，利用向量法能求出二面角D-A₁B-C₁的大小．

解答： （1）解：连结D₁C，AC，则△AD₁C是等边三角形，
∵A₁B∥D₁C，
∴异面直线AD₁与A₁B所成的角为∠AD₁C，
∵△AD₁C是等边三角形，
∴∠AD₁C=60°，
∴异面直线AD₁与A₁B所成的角为60°．
（2）证明：由（1）知A₁B∥D₁C，
∵A₁B不包含于平面AD₁C，D₁C?平面AD₁C，
∴直线A₁B∥平面AD₁C．
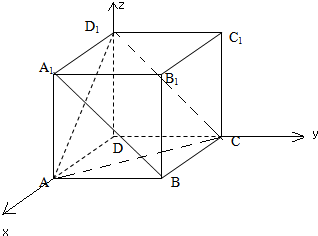
（3）解：以D为原点，建立空间直角坐标系，
设正方体ABCD-A₁B₁C₁D₁的棱长为1，
则D（0，0，0），A₁（1，0，1），B（1，1，0），C₁（0，1，1），

DA1

=（1，0，1），

DB

=（1，1，0），
设平面DA₁B的法向量

n

=（a，b，c），
则

DA1 • n =a+c=0 DB • n =a+b=0

，取a=1，得

n

=（1，-1，-1），

BA1

=（0，-1，1），

BC1

=（-1，0，1），
设平面A₁BC₁的法向量

m

=(x，y，z)，
则

BA1 • m =-y+z=0 BC1 • m =-x+z=0

，
取x=1，得

m

=（1，1，1），
设二面角D-A₁B-C₁的大小为θ，
cosθ=|cos＜

n

，

m

＞|=|

1-1-1

3 × 3

|=

1

3

，
∴θ=arccos

1

3

．
∴二面角D-A₁B-C₁的大小为arccos

1

3

．

点评：本题考查直线与平面所成角的大小的求法，考查直线与平面平行的证明，考查二面角的大小的求法，解题时要注意空间思维能力的培养．