练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知直线经过椭圆的右焦点，交椭圆于点，，点为椭圆的左焦点，的周长为..

    （Ⅰ）求椭圆的标准方程；

    （Ⅱ）若直线与直线的倾斜角互补，且交椭圆于点、，，求证：直线与直线的交点在定直线上.

    【答案】（Ⅰ）（Ⅱ）见证明

    【解析】

    （Ⅰ）根据椭圆的性质及已知条件求出，即可得出椭圆的标准方程。

    （Ⅱ）设出直线和直线的直线方程，分别代入椭圆的标准方程，利用弦长公式和韦达定理得出、，根据 确定的值，联立直线和直线的方程得到点P的坐标，从而确定点P在定直线上。

    解：（Ⅰ）由已知，得，，，

    椭圆的标准方程.

    （Ⅱ）若直线的斜率不存在，则直线的斜率也不存在，这与直线与直线相交于点矛盾，所以直线的斜率存在.

    令，，，，，.

    将直线的方程代入椭圆方程得：，

    ，，

    同理，.

    由得，此时，，

    直线，

    ，即点的定直线上.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】某公司为了解广告投入对销售收益的影响，在若干地区各投入4万元广告费用，并将各地的销售收益绘制成频率分布直方图（如图所示）.由于工作人员失误，横轴的数据丢失，但可以确定横轴是从0开始计数的.

    （1）根据频率分布直方图计算图中各小长方形的宽度；

    （2）估计该公司投入4万元广告费用之后，对应销售收益的平均值（以各组的区间中点值代表该组的取值）；

    （3）该公司按照类似的研究方法，测得另外一些数据，并整理得到下表：

    广告投入x（单位：万元）

    1

    2

    3

    4

    5

    销售收益y（单位：万元）

    1

    3

    4

    7

    表中的数据显示，x与y之间存在线性相关关系，请将（2）的结果填入上表的空白栏，并计算y关于x的回归方程.

    回归直线的斜率和截距的最小二乘法估计公式分别为，.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司需要对所生产的三种产品进行检测，三种产品数量（单位：件）如下表所示：

    产品

    A

    B

    C

    数量（件）

    180

    270

    90

    采用分层抽样的方法从以上产品中共抽取6件.

    （1）求分别抽取三种产品的件数；

    （2）将抽取的6件产品按种类编号，分别记为，现从这6件产品中随机抽取2件.

    （ⅰ）用所给编号列出所有可能的结果；

    （ⅱ）求这两件产品来自不同种类的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某公司计划购买1台机器，该种机器使用三年后即被淘汰.在购进机器时，可以一次性额外购买几次维修服务，每次维修服务费用200元，另外实际维修一次还需向维修人员支付小费，小费每次50元.在机器使用期间，如果维修次数超过购机时购买的维修服务次数，则每维修一次需支付维修服务费用500元，无需支付小费.现需决策在购买机器时应同时一次性购买几次维修服务，为此搜集并整理了100台这种机器在三年使用期内的维修次数，得下面统计表：

    维修次数

    8

    9

    10

    11

    12

    频数

    10

    20

    30

    30

    10

    记x表示1台机器在三年使用期内的维修次数，y表示1台机器在维修上所需的费用（单位：元），表示购机的同时购买的维修服务次数.

    （1）若=10，求y与x的函数解析式；

    （2）若要求“维修次数不大于”的频率不小于0.8，求n的最小值；

    （3）假设这100台机器在购机的同时每台都购买10次维修服务，或每台都购买11次维修服务，分别计算这100台机器在维修上所需费用的平均数，以此作为决策依据，购买1台机器的同时应购买10次还是11次维修服务？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（本小题满分10分）如图，已知四棱锥的底面是菱形，对角线交于点，，，，底面，设点满足．

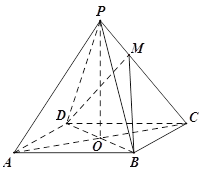
    （1）当时，求直线与平面所成角的正弦值；

    （2）若二面角的大小为，求的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】地球海洋面积远远大于陆地面积，随着社会的发展，科技的进步，人类发现海洋不仅拥有巨大的经济利益，还拥有着深远的政治利益.联合国于第63届联合国大会上将每年的6月8日确定为“世界海洋日”.2019年6月8日，某大学的行政主管部门从该大学随机抽取100名大学生进行一次海洋知识测试，并按测试成绩（单位：分）分组如下：第一组[65，70），第二组[70，75），第二组[75，80），第四组[80，85），第五组[85，90]，得到频率分布直方图如下图：

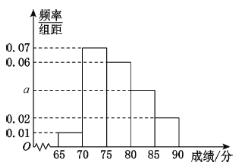
    （1）求实数的值；

    （2）若从第四组、第五组的学生中按组用分层抽样的方法抽取6名学生组成中国海洋实地考察小队，出发前，用简单随机抽样方法从6人中抽取2人作为正、副队长，列举出所有的基本事件并求“抽取的2人为不同组”的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，，圆C的方程为，过点A的直线l与圆C相切，点P为圆C上的动点.

    （1）求直线l的方程；

    （2）求面积的最大值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列命题中，正确的共有（ ）

    ① 因为直线是无限的，所以平面内的一条直线就可以延伸到平面外去；

    ② 两个平面有时只相交于一个公共点；

    ③ 分别在两个相交平面内的两条直线如果相交，则交点只可能在两个平面的交线上；

    ④ 一条直线与三角形的两边都相交，则这条直线必在三角形所在的平面内；

    A.0个B.1个C.2个D.3个

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在三棱柱中，侧面是菱形，，是棱的中点，，在线段上，且.

    （1）证明：面；

    （2）若，面面，求二面角的余弦值．

    查看答案和解析>>

    同步练习册答案