
分析 (1)先求导得到函数为单调递减,再求出(1)f(e2)<0,问题得以证明.
(2)由(1)可知,f(x)在∈[$\frac{1}{e}$,1]上单调递减,f(x)在∈[$\frac{1}{e}$,1]上的最小值为f(1)=1,只需t3-t2-2at+2≤1,即2a≥t2-t+$\frac{1}{t}$对任意的t∈[$\frac{1}{2}$,2]恒成立,
令g(t)=t2-t+$\frac{1}{t}$,利用导数求得g(t)的最大值,列出不等式即可求得结论.
解答 解:(1)∵f(x)=-$\frac{1}{2}$lnx+$\frac{2}{x+1}$,
∴f(x)的定义域为(0,+∞)
∴f′(x)=-$\frac{1}{2x}$-$\frac{2}{(x+1)^{2}}$<0,
∴f(x)在(0,+∞)单调递减,
∵f(1)=1>0,f(e2)=-$\frac{1}{2}$lne2+$\frac{2}{{e}^{2}+1}$=-1+$\frac{2}{{e}^{2}+1}$<0,
∴f(1)f(e2)<0,
∴f(x)在(1,e2)存在唯一的一个零点,
∴函数f(x)有且只有一个零点;
(2)由(1)可知,f(x)在∈[$\frac{1}{e}$,1]上单调递减,
∴f(x)在∈[$\frac{1}{e}$,1]上的最小值为f(1)=1,
∴只需t3-t2-2at+2≤1,即2a≥t2-t+$\frac{1}{t}$对任意的t∈[$\frac{1}{2}$,2]恒成立,
令g(t)=t2-t+$\frac{1}{t}$则g′(t)=2t-1-$\frac{1}{{t}^{2}}$=$\frac{2{t}^{3}-{t}^{2}-1}{{t}^{2}}$,
∵t∈[$\frac{1}{2}$,2],∴2t3-t2-1=(t-1)(2t2+t+1),
∴在t∈[$\frac{1}{2}$,1]上g(t)单调递减,在[1,2]上g(t)单调递增,
又g($\frac{1}{2}$)=$\frac{7}{4}$,g(2)=$\frac{5}{2}$,
∴g(t)在[,2]上的最大值是$\frac{5}{2}$,
∴只需2a≥$\frac{5}{2}$,即a≥$\frac{5}{4}$,
∴实数a的取值范围是[$\frac{5}{4}$,+∞).
点评 本题主要考查导函数零点存在定理,导数求函数的单调区间、最值等知识,考查学生恒成立问题的等价转化能力及运算求解能力,属于难题.


科目:高中数学 来源: 题型:解答题
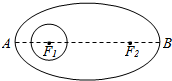 1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.
1998年12月19日,太原卫星发射中心为摩托罗拉公司(美国)发射了“铱星”系统通信卫星,卫星运行的轨道是椭圆,F1、F2是其焦点,地球中心为焦点F1,设地球半径为m,已知椭圆轨道的近地点A(离地面最近的点)距地面$\frac{m}{3}$,远地点B(离地面最远的点)距地面3m,并且F1、A、B在同一直线上,求卫星运行的轨道方程.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)+g(x)及f(x)•g(x)均为增函数 | |
| B. | f(x)-g(x)为增函数,f(x)•g(x)的增减性无法确定 | |
| C. | f(x)+g(x)及$\frac{f(x)}{φ(x)}$均为增函数 | |
| D. | f2(x)为增函数,$\frac{1}{φ(x)}$为增函数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (0,1) | B. | (1,+∞) | C. | (-1,0) | D. | (-∞,-1) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com