练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知分别是双曲线E： 的左、右焦点，P是双曲线上一点， 到左顶点的距离等于它到渐近线距离的2倍，（1）求双曲线的渐近线方程；（2）当时， 的面积为，求此双曲线的方程。

    【答案】（1）（2）

    【解析】试题分析：（1）由到左顶点的距离等于它到渐近线距离的倍，根据点到直线距离公式可得，从而可得双曲线的渐近线方程；（2）由余弦定理，结合双曲线的定义可得，再根据的面积为，可得，得，从而可得结果.

    试题解析：（1）因为双曲线的渐近线方程为，则点到渐近线距离为（其中c是双曲线的半焦距），所以由题意知，又因为，解得，故所求双曲线的渐近线方程是.

    （2）因为，由余弦定理得，即。又由双曲线的定义得，平方得，相减得。

    根据三角形的面积公式得，得。再由上小题结论得，故所求双曲线方程是.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】设p：不等式x2+（m﹣1）x+1＞0的解集为R；q：x∈（0，+∞），m≤x+ 恒成立．若“p且q”为假命题，“p或q”为真命题，求实数m的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知椭圆的左、右顶点分别为A，B，直线l斜率大于0，且l经过椭圆的右焦点F，与椭圆交于两点P，Q，若△AFP，△BFQ的面积分别为S1，S2，若，则直线l的斜率为_____．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设，是两条不同的直线， ，是两个不同的平面，则下列命题中正确的是

    A. 若，∥，∥, 则

    B. 若，，，则

    C. 若∥，， ，则

    D. 若∥， ，，则

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，已知A，B，C，D四点共面，且CD=1，BC=2，AB=4，∠ABC=120°，cos∠BDC= ．

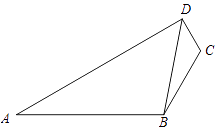
    （1）求sin∠DBC；
    （2）求AD．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数f（x）=ex（x2﹣a），a∈R．
    （1）当a=1时，求曲线y=f（x）在点（0，f（0））处的切线方程；
    （2）若函数f（x）在（﹣3，0）上单调递减，试求a的取值范围；
    （3）若函数f（x）的最小值为﹣2e，试求a的值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】抛物线的顶点为坐标原点O，焦点F在轴正半轴上，准线与圆相切.

    （Ⅰ）求抛物线的方程；

    （Ⅱ）已知直线和抛物线交于点，命题：“若直线过定点（0，1），则 ”，

    请判断命题的真假，并证明.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】椭圆C： =1的右焦点F，过焦点F的直线l0⊥x轴，P（x0 ， y0）（x0y0≠0）为C上任意一点，C在点P处的切线为l，l与l0相交于点M，与直线l1：x=3相交于N．
    （I） 求证；直线 =1是椭圆C在点P处的切线；
    （Ⅱ）求证： 为定值，并求此定值；
    （Ⅲ）请问△ONP（O为坐标原点）的面积是否存在最小值？若存在，请求出最小及此时点P的坐标；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】命题p：α∈R，sin（π﹣α）=cosα；命题q：“0＜a＜4”是“关于x的不等式ax2+ax+1＞0的解集是实数集R”的充分必要条件，则下面结论正确的是（ ）
    A.p是假命题
    B.q是真命题
    C.“p∧q”是假命题
    D.“p∨q”是假命题

    查看答案和解析>>

    同步练习册答案