
����Ŀ����֪ԲC1����x+2��2+��y��1��2=4��ԲC2����x��3��2+��y��4��2=4������P����1��5�����������ഹֱ��ֱ��l1��y=k��x+1��+5��l2��y=�� ![]() ��x+1��+5��
��x+1��+5��
��1����k=2ʱ����l1��ԲC1����A��B���㣬��A��B���������С��Բ�ķ��̣�
��2����l1��ԲC1�ཻ����֤��l2��ԲC2�ཻ����l1��ԲC1�صõ��ҳ���l2��ԲC2�صõ��ҳ���ȣ�
��3���Ƿ���ڵ�Q����Q���������б��֮��Ϊ1��ֱ��l3 �� l4 �� l3��ԲC1�صõ��ҳ���l4��ԲC2�صõ��ҳ���ȣ���������Q�����꣬�������ڣ�˵�����ɣ�
���𰸡�
��1���⣺��k=2ʱ��l1�ķ���Ϊy=2x+7
���������� ![]() ��������5x2+28x+36=0
��������5x2+28x+36=0
��A��BΪA��x1��y1����B��x2��y2���� ![]() ��
�� ![]() ��
�� ![]() ��
�� ![]() ��
��
����A��B���������С��ԲӦ����ABΪֱ����Բ��
Բ�ķ���Ϊ��x��x1����x��x2��+��y��y1����y��y2��=0��
��x2+y2����x1+x2��x����y1+y2��y+x1x2+y1y2=0
����Բ�ķ��̣� ![]()
��2���⣺��ԲC1��Բ�ĵ�l1�ľ���Ϊd1��ԲC2��Բ�ĵ�l2�ľ���Ϊd2���� ![]()
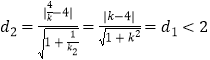 ��
��
��l2��ԲC2�ཻ��
����Բ�İ뾶��ȣ��������ľ���ȣ�
�����صõ��ҳ���ȣ�
��3���⣺��Q��a��b��3�ķ���Ϊy=m��x��a��+b��l4�ķ���Ϊ ![]() ��
��
������ԲC1��Բ�ĵ�l3�ľ���Ϊ ![]() ��
�� 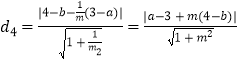
��d3=d4��|1��b+m��a+2��|=|a��3+m��4��b��|
��1��b+m��a+2��=a��3+m��4��b����
��1��b+m��a+2��=3��a+m��b��4����
�٢ڶ����������m��ֵ������
�� ![]() ��
��
�� ![]() ��
��
�ۢܶ����Q������
����������1������A��B���������С��ԲӦ����ABΪֱ����Բ����2��֤��l2��ԲC2�ཻ��������Բ�İ뾶��ȣ��������ľ���ȣ��ɵ����صõ��ҳ���ȣ���3����d3=d4��|1��b+m��a+2��|=|a��3+m��4��b��|��1��b+m��a+2��=a��3+m��4��b���ٻ�1��b+m��a+2��=3��a+m��b��4���ڣ��٢ڶ����������m��ֵ�������� ![]() �ۻ�
�ۻ� ![]() �ܣ��ۢܶ��⣬���ɵó����ۣ�
�ܣ��ۢܶ��⣬���ɵó����ۣ�


 ǧ�������������ĩ�����Ծ�����ϵ�д�
ǧ�������������ĩ�����Ծ�����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��l�ķ���Ϊ��2��m��x+��2m+1��y+3m+4=0������m��R��
��1����֤��ֱ��l������㣻
��2����m�仯ʱ�����P��3��1����ֱ��l�ľ�������ֵ��
��3����ֱ��l�ֱ���x�ᡢy��ĸ����ύ��A��B���㣬���AOB�������Сֵ����ʱֱ��l�ķ��̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪t= ![]() ��u��1�����ҹ���t�IJ���ʽt2��8t+m+18��0�н⣬��ʵ��m��ȡֵ��Χ�ǣ� ��
��u��1�����ҹ���t�IJ���ʽt2��8t+m+18��0�н⣬��ʵ��m��ȡֵ��Χ�ǣ� ��
A.�����ޣ���3��
B.����3��+�ޣ�
C.��3��+�ޣ�
D.�����ޣ�3��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ƽ��ֱ������ϵxOy�У�A��2��4����B����1��2����C��DΪ���㣬
��1����C��3��1������ƽ���ı���ABCD�������Խ��ߵij���
��2����C��a��b������ ![]() ����
���� ![]() ȡ����Сֵʱa��b��ֵ��
ȡ����Сֵʱa��b��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��������{an}�У�a1=1an+1= ![]() ��n��N*��
��n��N*��
��1����֤���� ![]() Ϊ�ȱ����У�
Ϊ�ȱ����У�
��2��������{an}��ǰn���Sn ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ͼ�ij����ͼ��ʾ���㷨�У���������ʵ��a��b��c��Ҫ�������x����������������������ô�ڿհ��жϿ��У�Ӧ�����루 �� 
A.x��c
B.c��x
C.c��b
D.c��a
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�Ȳ�����{an}�͵ȱ�����{bn}������{an}�Ĺ��Ϊ0����Sn������{an}��ǰn��ͣ���a1 �� a2 �� a5������{bn}��ǰ3���S4=16��
��1��������{an}��{bn}��ͨ�ʽ��
��2��������{ ![]() }Ϊ�Ȳ����У���ʵ��t��
}Ϊ�Ȳ����У���ʵ��t��
��3����������a1 �� b1 �� a2 �� b1 �� b2 �� a3 �� b1 �� b2 �� b3 �� ����ak �� b1 �� b2 �� ����bk �� ������������ǰn���Tn=1821����n��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾ���ڳ�����ABCD��A1B1C1D1�У�AB=AD=1��AA1=2��M����CC1���е㣮 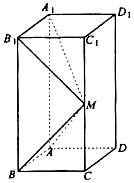
��1��֤����B1M��ƽ��ABM��
��2��������ֱ��A1M��C1D1���ɽǵ�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ڡ�ABC�У��ڽ�A��B��C���Եı߷ֱ�Ϊa��b��c����֪���� ![]() ��
�� ![]() ����
���� ![]() ��
��
��1�����B�Ĵ�С��
��2����b=2����ABC�����Ϊ ![]() ����a+c��ֵ��
����a+c��ֵ��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com