
【题目】下列四组函数,两个函数相同的是( )
A.f(x)= ![]() ,g(x)=x
,g(x)=x
B.f(x)=log33x , g(x)= ![]()
C.f(x)=( ![]() )2 , g(x)=|x|
)2 , g(x)=|x|
D.f(x)=x,g(x)=x0
【答案】B
【解析】解:对于A:f(x)= ![]() =|x|的定义域为R,g(x)=x的定义域为R,它们定义域相同,对应关系不相同,∴不是同一函数; 对于B:f(x)=log33x=x与g(x)=
=|x|的定义域为R,g(x)=x的定义域为R,它们定义域相同,对应关系不相同,∴不是同一函数; 对于B:f(x)=log33x=x与g(x)= ![]() =x它们的定义域相同,对应关系也相同,∴是同一函数;
=x它们的定义域相同,对应关系也相同,∴是同一函数;
对于C:f(x)=( ![]() )2的定义域为{x|x≥0},而g(x)=|x|的定义域为R,它们定义域不相同,∴不是同一函数;
)2的定义域为{x|x≥0},而g(x)=|x|的定义域为R,它们定义域不相同,∴不是同一函数;
对于D:f(x)=x的定义域为R,而g(x)=x0的定义域为{x|x≠0}.它们定义域不相同,∴不是同一函数;
故选B.
【考点精析】本题主要考查了判断两个函数是否为同一函数的相关知识点,需要掌握只有定义域和对应法则二者完全相同的函数才是同一函数才能正确解答此题.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,两焦点分别为
,两焦点分别为![]() ,右顶点为
,右顶点为![]() ,
, ![]() .
.
(Ⅰ)求椭圆![]() 的标准方程;
的标准方程;
(Ⅱ)设过定点![]() 的直线
的直线![]() 与双曲线
与双曲线![]() 的左支有两个交点,与椭圆
的左支有两个交点,与椭圆![]() 交于
交于![]() 两点,与圆
两点,与圆![]() 交于
交于![]() 两点,若
两点,若![]() 的面积为
的面积为![]() ,
, ![]() ,求正数
,求正数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种商品价格与该商品日需求量之间的几组对照数据如下表:

(1)求关于的线性回归方程;
(2)利用(1)中的回归方程,当价格![]() 元
元![]() 时,日需求量
时,日需求量![]() 的预测值为多少?
的预测值为多少?
参考公式:线性归回方程: ![]() ,其中
,其中 ,
, ![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】现有5名男司机,4名女司机,需选派5人运货到吴忠.
(1)如果派3名男司机、2名女司机,共有多少种不同的选派方法?
(2)至少有两名男司机,共有多少种不同的选派方法?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位共有10名员工,他们某年的收入如下表:
员工编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
年薪(万元) | 4 | 4.5 | 6 | 5 | 6.5 | 7.5 | 8 | 8.5 | 9 | 51 |
(1)求该单位员工当年年薪的平均值和中位数;
(2)从该单位中任取2人,此2人中年薪收入高于7万的人数记为![]() ,求
,求![]() 的分布列和期望;
的分布列和期望;
(3)已知员工年薪收入与工作年限成正相关关系,某员工工作第一年至第四年的年薪分别为4万元,5.5万元,6万元,8.5万元,预测该员工第五年的年薪为多少?
附:线性回归方程![]() 中系数计算公式分别为:
中系数计算公式分别为:
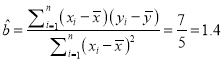 ,
, ![]() ,其中
,其中![]() 为样本均值.
为样本均值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某电子公司开发一种智能手机的配件,每个配件的成本是15元,销售价是20元,月平均销售![]() 件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为
件,通过改进工艺,每个配件的成本不变,质量和技术含金量提高,市场分析的结果表明,如果每个配件的销售价提高的百分率为![]() ,那么月平均销售量减少的百分率为
,那么月平均销售量减少的百分率为![]() ,记改进工艺后电子公司销售该配件的月平均利润是
,记改进工艺后电子公司销售该配件的月平均利润是![]() (元).
(元).
(1)写出![]() 与
与![]() 的函数关系式;
的函数关系式;
(2)改进工艺后,试确定该智能手机配件的售价,使电子公司销售该配件的月平均利润最大.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】选修4—4:坐标系与参数方程
在平面直角坐标系xOy中,曲线C1的参数方程为![]() (t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:
(t为参数).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2: ![]() .
.
(Ⅰ)求曲线C1和C2的直角坐标方程,并分别指出其曲线类型;
(Ⅱ)试判断:曲线C1和C2是否有公共点?如果有,说明公共点的个数;如果没有,请说明理由;
(Ⅲ)设![]() 是曲线C1上任意一点,请直接写出a + 2b的取值范围.
是曲线C1上任意一点,请直接写出a + 2b的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com