
【题目】某单位对一岗位面向社会公开招聘,若甲笔试成绩与面试成绩至少有一项比乙高,则称甲不亚于乙.在18位应聘者中,如果某应聘者不亚于其他17人,则称其为“优秀人才”.那么这18人中“优秀人才”数最多为( )
A. 1 B. 2 C. 9 D. 18
【答案】D
【解析】先考虑两个应聘者的情形,如果甲的笔试成绩>乙的笔试成绩,且乙的面试成绩>甲的面试成绩,可知“优秀人才”最多有2人.
再考虑三个应聘者的情形,如果甲的笔试成绩>乙的笔试成绩>丙的笔试成绩,且丙的面试成绩>乙的面试成绩>甲的面试成绩,可知“优秀人才”最多有3人.
由此可以设想,当有18个应聘者时,设每个应聘者为Ai,(i=1,2,…,100),其笔试成绩为xi,面试成绩为yi,当 ![]() 且
且![]() 时,由笔试成绩看,Ai不亚于Ai+1,Ai+2,…,A100;
时,由笔试成绩看,Ai不亚于Ai+1,Ai+2,…,A100;
由面试成绩看,Ai不亚于Ai-1,Ai-2,…,A1 所以,Ai不亚于其他17人(i=1,2,…,18)所以,Ai为“优秀人才”(i=1,2,…,18)
因此,18个应聘者中的“优秀人才”最多可能有 18个.
故选D.


 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案科目:高中数学 来源: 题型:
【题目】现有年龄在25到55岁的一群人身体上的某项数据,其频率分布直方图如下.(注:每组包括左端点,不包括右端点)

(1)请补全频率分布直方图;
(2)估计年龄的平均数;(精确到小数点后一位数字)
(3)若50到55岁的人数是50,现在想要从25到35岁的人群中用分层抽样的方法抽取30人,那么25到30岁这一组人中应该抽取多少人?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且当x≥0时,f(x)=loga(x+1)(a>0,且a≠1).
(1)求函数f(x)的解析式;
(2)若-1<f(1)<1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)= ![]() x3-
x3-![]() ax2,a∈R.
ax2,a∈R.
(1)当a=2时,求曲线y=f(x)在点(3,f(3))处的切线方程;
(2)设函数g(x)=f(x)+(x-a)cos x-sin x,讨论g(x)的单调性并判断有无极值,有极值时求出极值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某厂生产一种机器的固定成本为0.5万元,但每生产100台,需要加可变成本(即另增加投入)0.25万元,市场对此产品的年求量为500台,销售的收入函数为![]() (万元)(
(万元)(![]() ),其中
),其中![]() 是产品售出的数量(单位:百台).
是产品售出的数量(单位:百台).
(1)把利润表示为年产量的函数;
(2)年产量是多少时,工厂所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C过点M(0,-2)、N(3,1),且圆心C在直线x+2y+1=0上.
(1)求圆C的方程;
(2)设直线ax-y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2019年是新中国成立70周年,也是全面建成小康社会的关键之年.为喜迎祖国70周年生日,全民齐心奋力建设小康社会,某校特举办“喜迎国庆,共建小康”知识竞赛活动.下面的茎叶图是参赛两组选手的答题得分情况,则下列说法正确的是( )
甲 | 乙 | |||||
5 | 7 | 7 | ||||
7 | 3 | 2 | 8 | 3 | 4 | 5 |
3 | 9 | 1 | ||||
A.甲组选手得分的平均数小于乙组选手得分的平均数.
B.甲组选手得分的中位数大于乙组选手得分的平均数.
C.甲组选手得分的中位数等于乙组选手得分的中位数.
D.甲组选手得分的方差大于乙组选手得分的方差.
查看答案和解析>>
科目:高中数学 来源: 题型:
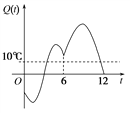
【题目】某地一年的气温Q(t)(单位:℃)与时间t(月份)之间的关系如图所示,已知该年的平均气温为10 ℃,令C(t)表示时间段[0,t]的平均气温,下列四个函数图象中,最能表示C(t)与t之间的函数关系的是( )
A.  B.
B.  C.
C.  D.
D. 
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆![]() 的圆心
的圆心![]() 在抛物线
在抛物线![]() 上,圆
上,圆![]() 过原点且与抛物线的准线相切.
过原点且与抛物线的准线相切.
(1)求该抛物线的方程;
(2)过抛物线焦点![]() 的直线
的直线![]() 交抛物线于
交抛物线于![]() ,
, ![]() 两点,分别在点
两点,分别在点![]() ,
, ![]() 处作抛物线的两条切线交于
处作抛物线的两条切线交于![]() 点,求三角形
点,求三角形![]() 面积的最小值及此时直线
面积的最小值及此时直线![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com