本题考查直线与平面垂直的判定,直线与平面所成的角,考查逻辑思维能力,空间想象能力,是中档题.
(1)因为DE∥BC.可以推理证明DE∥平面ACD
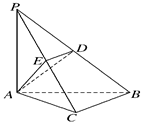
(2)要证BC⊥平面PAC,只需证明BC垂直平面PAC内的两条相交直线PA、AC即可;
(3)D为PB的中点,作出AD与平面PAC所成的角∠DAE,然后求其余弦值即可
解:(1)略 。。。。。。。。4分
(2)∵PA⊥底面ABC,∴PA⊥BC.
又∠BCA=90°,∴AC⊥BC,∴BC⊥平面PAC.。。。。。。。。。9分
(3)∵D为PB的中点,DE∥BC, ∴DE=
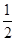
BC.
又由(1)知,BC⊥平面PAC, ∴DE⊥平面PAC,垂足为点E,
∴∠DAE是AD与平面PAC所成的角.。。。。。。。。。。。。。。。。。。11分
∵PA⊥底面ABC,∴PA⊥AB.
又PA=AB,∴△ABP为等腰直角三角形,∴AD=
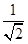
AB.
在Rt△ABC中,∠ABC=60°,∴BC=
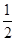
AB,
∴在Rt△ADE中,sin∠DAE=
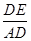
=
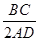
=
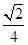
,
即AD与平面PAC所成角的正弦值为
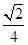
.。。。。。。。。。。。。。。。。14分

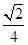 .
.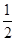 BC.
BC.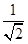 AB.
AB.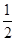 AB,
AB,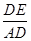 =
=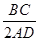 =
=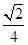 ,
,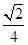 .。。。。。。。。。。。。。。。。14分
.。。。。。。。。。。。。。。。。14分


 ,直线PB与CD所成角为
,直线PB与CD所成角为 ,
,