
����Ŀ����ͼ,ijС��Ϊ��������,����������,�ƻ���һ��뾶ΪR��RΪ������������������,�������εĻ�̳CDEF��һ�������ε�ˮ��FCG.����![]() ,OΪԲ��,
,OΪԲ��,![]() ,C,G,F������Բ����,D,E�ֱ��ڰ뾶OA,OB��,��OG��CF,DE�ֱ���M,N,
,C,G,F������Բ����,D,E�ֱ��ڰ뾶OA,OB��,��OG��CF,DE�ֱ���M,N,![]() .
.
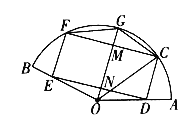
��1�����FCG�����S����![]() �Ĺ�ϵʽ,��д��������
�Ĺ�ϵʽ,��д��������
��2����R=10��,��̳ÿƽ���������300Ԫ,���ʾ��λ�̳���������Ƕ��٣���ȡ![]() ��
��
���𰸡�(1) ![]() . (2)17320Ԫ
. (2)17320Ԫ
��������
��1������Բ�ļ�������֤��![]() ������
������![]() ��ʾ��
��ʾ��![]() ���ɴ����������
���ɴ����������![]() ����ı���ʽ�������
����ı���ʽ�������![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��2�����![]() ���ɴ���þ���
���ɴ���þ���![]() ����ı���ʽ�����ø����ǹ�ʽ��������Ǻ�������ֵ�ķ�������þ���
����ı���ʽ�����ø����ǹ�ʽ��������Ǻ�������ֵ�ķ�������þ���![]() ��������ֵ���Ӷ����������.
��������ֵ���Ӷ����������.
��1������OF,��Ϊ![]() ,����
,����![]() ,��
,��![]() ,����
,����![]() .
.
��Ϊ![]() ,����
,����![]() ,����
,����![]() ,
,![]() ,
,
����![]() .
.
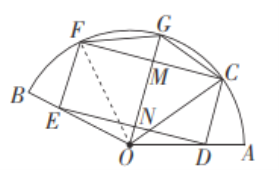
��2����Ϊ![]() ,
,
����![]() ,
,
����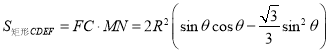
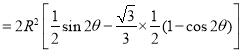
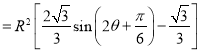 .
.
��Ϊ![]() ,���Ե�
,���Ե�![]() ʱ,
ʱ,![]() ���.
���.
�ʾ��λ�̳����������![]() Ԫ.
Ԫ.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����![]() ���������ƽ���õ�������λ���ȣ�����
���������ƽ���õ�������λ���ȣ�����![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() ��
��![]() �����Ƶ�ʷֲ�ֱ��ͼ��ͼ��
�����Ƶ�ʷֲ�ֱ��ͼ��ͼ��

��1����ֱ��ͼ��![]() ��ֵ��
��ֵ��
��2������ƽ���õ�������������λ����
��3������ƽ���õ���Ϊ![]() ��
��![]() ��
��![]() ��
��![]() �������û��У��÷ֲ�����ķ�����ȡ
�������û��У��÷ֲ�����ķ�����ȡ![]() ����������ƽ���õ�����
����������ƽ���õ�����![]() ���û���Ӧ��ȡ���ٻ���
���û���Ӧ��ȡ���ٻ���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ź�����Ѿ���Ϊ�й����ջ��ȴ���ʱ�dz�ϲ����һ����С���ռ�����20��ͬѧ���괺���ڼ�����������![]() ��Ԫ�����£���������ȡ��������
��Ԫ�����£���������ȡ��������
102 52 41 121 72
162 50 22 158 46
43 136 95 192 59
99 22 68 98 79
����20�����ݽ��з��飬�����Ƶ�����£�
��� | ��������� | Ƶ�� |
|
| 2 |
|
| 9 |
|
|
|
|
| 3 |
|
|
|
������д����ֵ�����ش���20��ͬѧ�����ĺ��������λ�������ĸ����
��������![]() ��������ƽ�����뷽��ֱ�Ϊ
��������ƽ�����뷽��ֱ�Ϊ![]() ��������ƽ�����뷽��ֱ�Ϊ
��������ƽ�����뷽��ֱ�Ϊ![]() ���Էֱ�Ƚ�
���Էֱ�Ƚ�![]() ��
��![]() ��
��![]() ��
��![]() �Ĵ�С����ֻ��д�����ۣ�
�Ĵ�С����ֻ��д�����ۣ�
��������![]() �����������������ȡ2�����ݣ�����2�����ݲ�ľ���ֵΪ
�����������������ȡ2�����ݣ�����2�����ݲ�ľ���ֵΪ![]() ����
����![]() �ķֲ��к���ѧ������
�ķֲ��к���ѧ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������ABC�У�
��1����֤��cos2![]() +cos2
+cos2![]() =1��
=1��
��2����cos��![]() +A��sin��
+A��sin��![]() ��+B��tan��C���У���0����֤����ABCΪ�۽������Σ�
��+B��tan��C���У���0����֤����ABCΪ�۽������Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����![]() (n��2)��ʵ����ɵ�n��n�е������У�
(n��2)��ʵ����ɵ�n��n�е������У� ![]() ��ʾ��i�е�j�е�������
��ʾ��i�е�j�е�������![]() ��
�� ![]() ��
��![]() ��-1,0,1} (
��-1,0,1} (![]() )����r1,r2,��,rn,c1,c2,..,cn���������ȣ���ƴ˱�Ϊ��n��H��������
)����r1,r2,��,rn,c1,c2,..,cn���������ȣ���ƴ˱�Ϊ��n��H��������
H={ r1,r2,��,rn,c1,c2,..,cn}.
(I����д��һ����2��H����;
(II��������һ����n��H������������![]() ����
����![]() ����֤��
����֤�� ![]() Ϊż����
Ϊż����
(����֤�������ڡ�5��H����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��![]() ���Һ���
���Һ���![]() ��ż����.
��ż����.
��1����![]() �Ľ���ʽ��
�Ľ���ʽ��
��2��������ʽ![]() ��
��![]() �Ϻ��������
�Ϻ��������![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
��3��������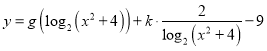 ǡ����������㣬��
ǡ����������㣬��![]() ��ֵ���ú��������.
��ֵ���ú��������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ȼ��Ч������ָ����ÿ����1��������ʻ����̣���ͼ�����˼ס��ҡ������������ڲ�ͬ�ٶ��µ�ȼ��Ч�����. ������������ȷ���ǣ� ��

A. ����1�����ͣ��ҳ�������ʻ5ǧ��
B. ����ͬ�ٶ���ʻ��ͬ·�̣��������У��׳������������
C. �׳���80ǧ��/Сʱ���ٶ���ʻ1Сʱ������10������
D. ij���л������������80ǧ��/Сʱ. ��ͬ�����£��ڸ����ñ��������ҳ���ʡ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ijУѧ��������֯��ḻ��ѧ����Ϊ�˽�ͬѧ�����Ż������̶ȣ����ѡȡ��100λͬѧ�����ʾ����飬�����ʾ��е���100�˸��������������ֵ���ٷ��ƣ�����[40��50����[50��60����[60��70��������[90��100]�ֳ�6�飬�Ƴ���ͼ��ʾƵ�ʷֲ�ֱ��ͼ��
��1����ͼ��x��ֵ��
��2�����������ݵ���λ����
��3���ִӱ�������ʾ����������ֵ��[60��80����ѧ���а��ֲ�����ķ�����ȡ5�˽�����̸�˽⣬�ٴ���5���������ȡ2�������ⷢ�ԣ����ȡ��2��ǡ��ͬһ��ĸ��ʣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() ��
��
��1����![]() ʱ������
ʱ������![]() ǡ��������ͬ����㣬��ʵ��
ǡ��������ͬ����㣬��ʵ��![]() ��ֵ��
��ֵ��
��2����![]() ʱ��
ʱ��
�� ����������![]() ������
������![]() ����
����![]() ��ȡֵ��Χ��
��ȡֵ��Χ��
�� ��![]() ������
������![]() ������
������![]() �ϵ����ֵ
�ϵ����ֵ![]() ��
��
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com