
 如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.
如图,正方形ABCD的中心为O,四边形OBEF为矩形,平面OBEF⊥平面ABCD,点G为AB的中点,AB=BE=2.分析 (1)取AD的中点I,连接FI,证明四边形EFIG是平行四边形,可得EG∥FI,利用线面平行的判定定理证明:EG∥平面ADF;
(2)建立如图所示的坐标系O-xyz,求出平面CEF的法向量,$\overrightarrow{BH}$,利用向量的夹角公式求出直线BH和平面CEF所成角的正弦值.
解答 (1)证明:取AD的中点I,连接FI,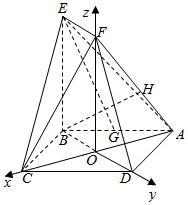
∵矩形OBEF,∴EF∥OB,EF=OB,
∵G,I是中点,
∴GI∥BD,GI=$\frac{1}{2}$BD.
∵O是正方形ABCD的中心,
∴OB=$\frac{1}{2}$BD.
∴EF∥GI,EF=GI,
∴四边形EFIG是平行四边形,
∴EG∥FI,
∵EG?平面ADF,FI?平面ADF,
∴EG∥平面ADF;
(2)解:建立如图所示的坐标系O-xyz,则B(0,-$\sqrt{2}$,0),C($\sqrt{2}$,0,0),E(0,-$\sqrt{2}$,2),
F(0,0,2),
设平面CEF的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\sqrt{2}y=0}\\{-\sqrt{2}x+2z=0}\end{array}\right.$,取$\overrightarrow{m}$=($\sqrt{2}$,0,1)
AH=$\frac{2}{3}$HF,∴$\overrightarrow{AH}$=($\frac{2\sqrt{2}}{5}$,0,$\frac{4}{5}$).
设H(a,b,c),则$\overrightarrow{AH}$=(a+$\sqrt{2}$,b,c)=($\frac{2\sqrt{2}}{5}$,0,$\frac{4}{5}$).
∴a=-$\frac{3\sqrt{2}}{5}$,b=0,c=$\frac{4}{5}$,
∴$\overrightarrow{BH}$=(-$\frac{3\sqrt{2}}{5}$,$\sqrt{2}$,$\frac{4}{5}$),
∴直线BH和平面CEF所成角的正弦值=|cos<$\overrightarrow{BH}$,$\overrightarrow{m}$>|=$\frac{|-\frac{6}{5}+\frac{4}{5}|}{\sqrt{3}•\sqrt{\frac{84}{25}}}$=$\frac{\sqrt{7}}{21}$.
点评 本题考查证明线面平行的判定定理,考查直线BH和平面CEF所成角的正弦值,考查学生分析解决问题的能力,属于中档题.


 课堂全解字词句段篇章系列答案
课堂全解字词句段篇章系列答案 步步高口算题卡系列答案
步步高口算题卡系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )
矩形ABCD中,$AB=\sqrt{3}$,BC=1,将△ABC与△ADC沿AC所在的直线进行随意翻折,在翻折过程中直线AD与直线BC成的角范围(包含初始状态)为( )| A. | $[0,\frac{π}{6}]$ | B. | $[0,\frac{π}{3}]$ | C. | $[0,\frac{π}{2}]$ | D. | $[0,\frac{2π}{3}]$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
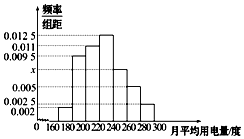
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
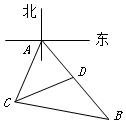 为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.
为了考核某特警部队的应急反应能力,拟准备把特警队员从一目标处快速运送到另一目标处.通过测角仪观测到观测站C在目标A南偏西25°的方向上,B、D在A出发的一条南偏东35°走向的公路上(如图),测得C、B相距31千米,D、B相距20千米,C、D相距21千米,求A、D之间的距离.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com