
【题目】已知集合![]() ,若对于任意
,若对于任意![]() ,存在
,存在![]() ,使得
,使得![]() 成立,则称集合是“好集合”.给出下列4个集合:①
成立,则称集合是“好集合”.给出下列4个集合:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中为“好集合”的序号是( )
.其中为“好集合”的序号是( )
A. ①②④ B. ②③ C. ③④ D. ①③④
【答案】B
【解析】对于①y=![]() 是以x,y轴为渐近线的双曲线,渐近线的夹角是90°,所以在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足好集合的定义;在另一支上对任意(x1,y1)∈M,不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,所以不满足好集合的定义,不是好集合.
是以x,y轴为渐近线的双曲线,渐近线的夹角是90°,所以在同一支上,任意(x1,y1)∈M,不存在(x2,y2)∈M,满足好集合的定义;在另一支上对任意(x1,y1)∈M,不存在(x2,y2)∈M,使得x1x2+y1y2=0成立,所以不满足好集合的定义,不是好集合.
对于②M={(x,y)|y=ex-2},如图(2)如图红线的直角始终存在,对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,例如取M(0,-1),则N(ln2,0),满足好集合的定义,
所以是好集合;正确.
对于③M={(x,y)|y=cosx},如图(3)对于任意(x1,y1)∈M,存在(x2,y2)∈M,使得x1x2+y1y2=0成立,例如(0,1)、(π,0),满足好集合的定义,所以M是好集合;正确.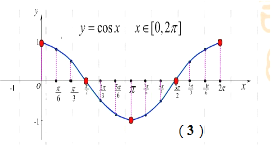
对于④M={(x,y)|y=lnx},如图(4)取点(1,0),曲线上不存在另外的点,使得两点与原点的连线互相垂直,所以不是好集合.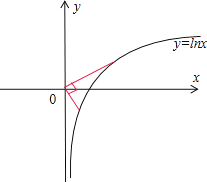
所以②③正确.
故选B.


科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的左焦点
的左焦点![]() 的离心率为
的离心率为![]() 是
是![]() 和
和![]() 的等比中项.
的等比中项.
(1)求曲线![]() 的方程;
的方程;
(2)倾斜角为![]() 的直线过原点
的直线过原点![]() 且与
且与![]() 交于
交于![]() 两点,倾斜角为
两点,倾斜角为![]() 的直线过
的直线过![]() 且与
且与![]() 交于
交于![]() 两点,若
两点,若![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,已知四边形ABCD是平行四边形,点P是平面ABCD外一点,M是PC的中点,在DM上取一点G,过G和AP作平面交平面BDM于GH.求证: 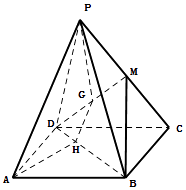
(1)AP∥平面BDM;
(2)AP∥GH.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com