
【题目】已知圆![]() ,一动圆与直线
,一动圆与直线![]() 相切且与圆
相切且与圆![]() 外切.
外切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)若经过定点![]() 的直线
的直线![]() 与曲线
与曲线![]() 交于
交于![]() 两点,
两点, ![]() 是线段
是线段![]() 的中点,过
的中点,过![]() 作
作![]() 轴的平行线与曲线
轴的平行线与曲线![]() 相交于点
相交于点![]() ,试问是否存在直线
,试问是否存在直线![]() ,使得
,使得![]() ,若存在,求出直线
,若存在,求出直线![]() 的方程,若不存在,说明理由.
的方程,若不存在,说明理由.
【答案】(1) ![]() ;(2) 存在直线
;(2) 存在直线![]() 或
或![]() ,使得
,使得![]() .
.
【解析】试题分析:
(1)本题用直接法求动点轨迹方程,设支点坐标为![]() ,当然由已知分析,动点不能在
,当然由已知分析,动点不能在![]() 轴左侧,然后利用直线与圆相切和两圆外切的条件列出方程,化简即可;
轴左侧,然后利用直线与圆相切和两圆外切的条件列出方程,化简即可;
(2)假设存在满足题意的直线,设出直线方程,分析发现直线的斜率为0时不合题意,从而设直线方程为![]() ,设
,设![]() ,直线方程与曲线方程联立方程组,消去变量
,直线方程与曲线方程联立方程组,消去变量![]() 后得
后得![]() 的一元二次方程,由韦达定理得
的一元二次方程,由韦达定理得![]() ,设
,设![]() ,得
,得![]() ,
, ![]() ,由
,由![]() 求出
求出![]() 值,得直线方程,若不能求出实数
值,得直线方程,若不能求出实数![]() ,则说明假设错误,不存在相应的直线.
,则说明假设错误,不存在相应的直线.
试题解析:
(1)设![]() ,分析可知:动圆的圆心不能在
,分析可知:动圆的圆心不能在![]() 轴的左侧,故
轴的左侧,故![]() ,
,
∵动圆与直线![]() 相切,且与圆
相切,且与圆![]() 外切,
外切,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
化简可得![]() ;
;
(2)设![]() ,
,
由题意可知,当直线![]() 与
与![]() 轴垂直时,显然不符合题意,
轴垂直时,显然不符合题意,
故可设直线![]() 的方程为
的方程为![]() ,
,
联立![]() 和
和![]() 并消去
并消去![]() ,可得
,可得![]() ,
,
显然![]() ,由韦达定理可知
,由韦达定理可知![]() ,①
,①
又∵![]() ,
,
∴![]() ,②
,②
∵![]() ,∴
,∴![]() ,③
,③
假设存在![]() ,使得
,使得![]() ,
,
由题意可知![]() ,∴
,∴![]() ,④
,④
由![]() 点在抛物线上可知
点在抛物线上可知![]() ,即
,即![]() ,⑤
,⑤
又![]() ,
,
若![]() ,则
,则![]() ,
,
由①②③④⑤代入上式化简可得![]() ,
,
即![]() ,
,
∴![]() ,故
,故![]() ,
,
∴存在直线![]() 或
或![]() ,使得
,使得![]() .
.


 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:高中数学 来源: 题型:
【题目】甲船在岛B的正南A处,AB=10千米.甲船以每小时4千米的速度向北航行,同时,乙船自B出发以每小时6千米的速度向北偏东60°的方向驶去.当甲船在A,B之间,且甲、乙两船相距最近时,它们所航行的时间是( )

A. ![]() 分钟 B.
分钟 B. ![]() 小时 C. 21.5分钟 D. 2.15分钟
小时 C. 21.5分钟 D. 2.15分钟
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱柱![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 为菱形,
为菱形, ![]() 为
为![]() 与
与![]() 交点,已知
交点,已知![]() ,
,![]() .
.

(Ⅰ)求证: ![]() 平面
平面![]() ;
;
(Ⅱ)求证: ![]() ∥平面
∥平面![]() ;
;
(Ⅲ)设点![]() 在
在![]() 内(含边界),且
内(含边界),且![]()
![]() ,说明满足条件的点
,说明满足条件的点![]() 的轨迹,并求
的轨迹,并求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 和抛物线
和抛物线![]() 有公共焦点
有公共焦点![]() ,
, ![]() 的中心和
的中心和![]() 的顶点都在坐标原点,过点
的顶点都在坐标原点,过点![]() 的直线
的直线![]() 与抛物线
与抛物线![]() 分别相交于
分别相交于![]() 两点(其中点
两点(其中点![]() 在第四象限内).
在第四象限内).
(1)若![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)若坐标原点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() 在抛物线
在抛物线![]() 上,直线
上,直线![]() 与椭圆
与椭圆![]() 有公共点,求椭圆
有公共点,求椭圆![]() 的长轴长的最小值.
的长轴长的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
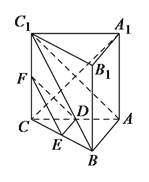
【题目】如图,在三棱柱![]() 中,
中,![]() 底面
底面![]() ,
,![]()
![]() ,
,![]() 、
、![]() 分别是棱
分别是棱![]() 、
、![]() 的中点.
的中点.
(Ⅰ)求证:![]() 平面
平面![]() .
.
(Ⅱ)若线段![]() 上的点
上的点![]() 满足平面
满足平面![]() 平面
平面![]() ,试确定点
,试确定点![]() 的位置,并说明理由.
的位置,并说明理由.
(Ⅲ)证明:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】对某地区儿童的身高与体重的一组数据,我们用两种模型①![]() ,②
,②![]() 拟合,得到回归方程分别为
拟合,得到回归方程分别为![]() ,
, ![]() ,作残差分析,如表:
,作残差分析,如表:
身高 | 60 | 70 | 80 | 90 | 100 | 110 |
体重 | 6 | 8 | 10 | 14 | 15 | 18 |
| 0.41 | 0.01 | 1.21 | -0.19 | 0.41 | |
| -0.36 | 0.07 | 0.12 | 1.69 | -0.34 | -1.12 |
(Ⅰ)求表中空格内的值;
(Ⅱ)根据残差比较模型①,②的拟合效果,决定选择哪个模型;
(Ⅲ)残差大于![]() 的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
的样本点被认为是异常数据,应剔除,剔除后对(Ⅱ)所选择的模型重新建立回归方程.
(结果保留到小数点后两位)
附:对于一组数据![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘法估计分别为
的斜率和截距的最小二乘法估计分别为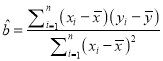 ,
, ![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com