
【题目】若![]() 是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
是两个相交平面,则在下列命题中,真命题的序号为 .(写出所有真命题的序号)
①若直线![]() ,则在平面
,则在平面![]() 内,一定不存在与直线
内,一定不存在与直线![]() 平行的直线.
平行的直线.
②若直线![]() ,则在平面
,则在平面![]() 内,一定存在无数条直线与直线
内,一定存在无数条直线与直线![]() 垂直.
垂直.
③若直线![]() ,则在平面
,则在平面![]() 内,不一定存在与直线
内,不一定存在与直线![]() 垂直的直线.
垂直的直线.
④若直线![]() ,则在平面
,则在平面![]() 内,一定存在与直线
内,一定存在与直线![]() 垂直的直线.
垂直的直线.
科目:高中数学 来源: 题型:
【题目】如图,在底面是正方形的四棱锥P﹣ABCD中,PA⊥面ABCD,BD交AC于点E,F是PC中点,G为AC上一点. 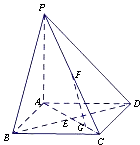
(1)求证:BD⊥FG;
(2)确定点G在线段AC上的位置,使FG∥平面PBD,并说明理由;
(3)当二面角B﹣PC﹣D的大小为 ![]() 时,求PC与底面ABCD所成角的正切值.
时,求PC与底面ABCD所成角的正切值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本题满分16分)数列![]() ,
, ![]() ,
, ![]() 满足:
满足: ![]() ,
, ![]() ,
, ![]() .
.
(1)若数列![]() 是等差数列,求证:数列
是等差数列,求证:数列![]() 是等差数列;
是等差数列;
(2)若数列![]() ,
, ![]() 都是等差数列,求证:数列
都是等差数列,求证:数列![]() 从第二项起为等差数列;
从第二项起为等差数列;
(3)若数列![]() 是等差数列,试判断当
是等差数列,试判断当![]() 时,数列
时,数列![]() 是否成等差数列?证明你的结论.
是否成等差数列?证明你的结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+ ![]() ﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln
﹣2)(a>0) (Ⅰ)当1<a<4时,函数f(x)在[2,4]上的最小值为ln ![]() ,求a;
,求a;
(Ⅱ)若存在x0∈(2,+∞),使得f(x0)<0,求a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图是我国南宋时期的数学家秦九韶提出的一种多项式f(x)=anxn+an﹣1xn﹣1+…+a1x+a0的求值问题的算法.现按照这个程序执行函数f (x)=3x4﹣2x3﹣6x﹣17的计算,若输入的值x0=2,则输出的v的值是( ) 
A.0
B.2
C.3
D.﹣3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在半径为 ![]() ,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ.
,圆心角为60°的扇形的弧上任取一点P,作扇形的内接矩形PNMQ,使点Q在OA上,点N,M在OB上,设矩形PNMQ的面积为y,∠POB=θ. 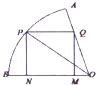
(1)将y表示成θ的函数关系式,并写出定义域;
(2)求矩形PNMQ的面积取得最大值时 ![]()
![]() 的值;
的值;
(3)求矩形PNMQ的面积y≥ ![]() 的概率.
的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=mex﹣x﹣1(其中e为自然对数的底数,),若f(x)=0有两根x1 , x2且x1<x2 , 则函数y=(e ![]() ﹣e
﹣e ![]() )(
)( ![]() ﹣m)的值域为 .
﹣m)的值域为 .
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从1开始的自然数按如图所示的规则排列,现有一个三角形框架在图中上下或左右移动,使每次恰有九个数在此三角形内,则这九个数的和可以为( )
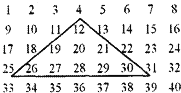
A.2097 B.2112 C.2012 D.2090
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com