
【题目】已知椭圆![]() 1(
1(![]() )的离心率为
)的离心率为![]() ,且经过点
,且经过点![]() ,直线
,直线![]()
![]() 与椭圆E交于B,C两点(B,C不与A重合).
与椭圆E交于B,C两点(B,C不与A重合).
(1)求椭圆E的方程;
(2)若O,B,C三点不共线时(O为坐标原点),求![]() 面积的最大值;
面积的最大值;
(3)设直线AB,AC与![]() 轴的交点分别为P,Q,求证:
轴的交点分别为P,Q,求证:![]() .
.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)证明见解析.
;(3)证明见解析.
【解析】
(1)结合待定系数法和离心率公式及椭圆的关系式联立解方程即可求解;
(2)联立直线与椭圆标准方程,由韦达定理得x1+x2=﹣m,![]() ,表示出弦长
,表示出弦长![]() ,由点到直线距离公式求得O到直线BC的距离d,结合面积公式化简可得S△OBC
,由点到直线距离公式求得O到直线BC的距离d,结合面积公式化简可得S△OBC ,由不等式性质可求最值;
,由不等式性质可求最值;
(3)画出图像,需将结论进行转化,要求![]() ,即求∠AQP=∠APQ,即证kAP+kAQ=0,即证kAB+kAC=0,结合(2)化简即可得证;
,即求∠AQP=∠APQ,即证kAP+kAQ=0,即证kAB+kAC=0,结合(2)化简即可得证;
(1)由题意可知: ,解得
,解得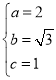 ,∴椭圆E的方程为:
,∴椭圆E的方程为:![]() ;
;
(2)由A不在l上,可知m≠1,由 ,得:x2+mx+m2﹣3=0,
,得:x2+mx+m2﹣3=0,
∴△=m2﹣4(m2﹣3)=12﹣3m2>0,即﹣2<m<2,且m≠1,m≠0,设B(x1,y1),C(x2,y2),
∴x1+x2=﹣m,![]() ,
,
∴|BC| ,
,
又∵点O到直线BC的距离d ,
,
∴S△OBC ,
,
当且仅当m![]() (满足△>0且m≠0,1)时,△OBC的面积取得最大值
(满足△>0且m≠0,1)时,△OBC的面积取得最大值![]() ;
;
(3)

由(2)可知x1+x2=﹣m,![]() ,∴kAP+kAQ=kAB+kAC
,∴kAP+kAQ=kAB+kAC 1
1![]()
1![]() 0,∴∠AQP=∠APQ,∴|AP|=|AQ|.
0,∴∠AQP=∠APQ,∴|AP|=|AQ|.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() ,且与直线
,且与直线![]() 相切.
相切.
(1)求动圆圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)设![]() 是轨迹
是轨迹![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的斜率分别为
的斜率分别为![]() ,且
,且![]() ,证明直线
,证明直线![]() 恒过定点,并求出该定点的坐标
恒过定点,并求出该定点的坐标
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】从某部门参加职业技能测试的2000名员工中抽取100名员工,将其成绩(满分100分)按照[50,60),[60,70),[70,80),[80,90),[90,100)分成5组,得到如图所示的频率分布直方图.

(1)估计该部门参加测试员工的成绩的众数中位数;
(2)估计该部门参加测试员工的平均成绩;
(3)若成绩在80分及以上为优秀,请估计该部门2000名员工中成绩达到优秀的人数为多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某种产品的质量以其质量指标值衡量,并依据质量指标值划分等级如下表:
![]()
从某企业生产的这种产品中抽取200件,检测后得到如下的频率分布直方图:
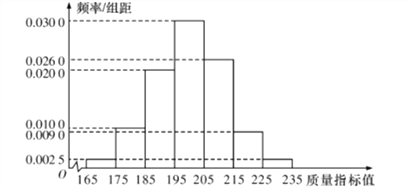
(1)根据以上抽样调查数据,能否认为该企业生产的这种产品符合“一、二等品至少要占全部产品![]() ”的规定?
”的规定?
(2)在样本中,按产品等级用分层抽样的方法抽取8件,再从这8件产品中随机抽取4件,求抽取的4件产品中,一、二、三等品都有的概率;
(3)该企业为提高产品质量,开展了“质量提升月”活动,活动后再抽样检测,产品质量指标值![]() 近似满足
近似满足![]() ,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
,则“质量提升月”活动后的质量指标值的均值比活动前大约提升了多少?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面四边形ABCD中, AB=2,BD=![]() ,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.
,AB⊥BC,∠BCD=2∠ABD,△ABD的面积为2.

(1)求AD的长;
(2)求△CBD的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com