
【题目】设直线系![]() (
(![]() ),则下列命题中是真命题的个数是( )
),则下列命题中是真命题的个数是( )
①存在一个圆与所有直线相交;
②存在一个圆与所有直线不相交;
③存在一个圆与所有直线相切;
④![]() 中所有直线均经过一个定点;
中所有直线均经过一个定点;
⑤不存在定点![]() 不在
不在![]() 中的任一条直线上;
中的任一条直线上;
⑥对于任意整数![]() ,存在正
,存在正![]() 边形,其所有边均在
边形,其所有边均在![]() 中的直线上;
中的直线上;
⑦![]() 中的直线所能围成的正三角形面积都相等.
中的直线所能围成的正三角形面积都相等.
A.3B.4C.5D.6
【答案】B
【解析】
根据已知可知,直线系![]() 都为以
都为以![]() 为圆心,以1为半径的圆的切线,即可根据相关知识,逐个判断各命题的真假.
为圆心,以1为半径的圆的切线,即可根据相关知识,逐个判断各命题的真假.
根据直线系![]() (
(![]() )得到,
)得到,
所有直线都为圆心为![]() ,半径为1的圆的切线.
,半径为1的圆的切线.
对于①,可取圆心为![]() ,半径为2的圆,该圆与所有直线相交,所以①正确;
,半径为2的圆,该圆与所有直线相交,所以①正确;
对于②,可取圆心为![]() ,半径为
,半径为![]() 的圆,该圆与所有直线不相交,所以②正确;
的圆,该圆与所有直线不相交,所以②正确;
对于③,可取圆心为![]() ,半径为1的圆,该圆与所有直线相切,所以③正确;
,半径为1的圆,该圆与所有直线相切,所以③正确;
对于④,所有的直线与一个圆相切,没有过定点,所以④错误;
对于⑤,存在![]() 不在
不在![]() 中的任一条直线上,所以⑤错误;
中的任一条直线上,所以⑤错误;
对于⑥,可取圆的外接正三角形,其所有边均在![]() 中的直线上,所以⑥正确;
中的直线上,所以⑥正确;
对于⑦,可以在圆的三等分点做圆的三条切线,把其中一条切线平移到过另外两个点中点时,也为正三角形,但是它与圆的外接正三角形的面积不相等,所以⑦错误;
故①②③⑥正确,④⑤⑦错,所以真命题的个数为4个.
故选:B.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】已知等差数列![]() 的首项为p,公差为
的首项为p,公差为![]() ,对于不同的自然数
,对于不同的自然数![]() ,直线
,直线![]() 与
与![]() 轴和指数函数
轴和指数函数![]() 的图象分别交于点
的图象分别交于点![]() 与
与![]() (如图所示),记
(如图所示),记![]() 的坐标为
的坐标为![]() ,直角梯形
,直角梯形![]() 、
、![]() 的面积分别为
的面积分别为![]() 和
和![]() ,一般地记直角梯形
,一般地记直角梯形![]() 的面积为
的面积为![]() .
.

(1)求证:数列![]() 是公比绝对值小于1的等比数列;
是公比绝对值小于1的等比数列;
(2)设![]() 的公差
的公差![]() ,是否存在这样的正整数
,是否存在这样的正整数![]() ,构成以
,构成以![]() ,
,![]() ,
,![]() 为边长的三角形?并请说明理由;
为边长的三角形?并请说明理由;
(3)设![]() 的公差
的公差![]() 为已知常数,是否存在这样的实数p使得(1)中无穷等比数列
为已知常数,是否存在这样的实数p使得(1)中无穷等比数列![]() 各项的和
各项的和![]() ?并请说明理由.
?并请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
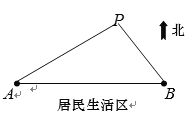
【题目】如图所示,![]() 、
、![]() 是两个垃圾中转站,
是两个垃圾中转站,![]() 在
在![]() 的正东方向
的正东方向![]() 千米处,
千米处,![]() 的南面为居民生活区.为了妥善处理生活垃圾,政府决定在
的南面为居民生活区.为了妥善处理生活垃圾,政府决定在![]() 的北面建一个垃圾发电厂
的北面建一个垃圾发电厂![]() .垃圾发电厂
.垃圾发电厂![]() 的选址拟满足以下两个要求(
的选址拟满足以下两个要求(![]() 、
、![]() 、
、![]() 可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点
可看成三个点):①垃圾发电厂到两个垃圾中转站的距离与它们每天集中的生活垃圾量成反比,比例系数相同;②垃圾发电厂应尽量远离居民区(这里参考的指标是点![]() 到直线
到直线![]() 的距离要尽可能大).现估测得
的距离要尽可能大).现估测得![]() 、
、![]() 两个中转站每天集中的生活垃圾量分别约为
两个中转站每天集中的生活垃圾量分别约为![]() 吨和
吨和![]() 吨.设
吨.设![]() .
.
(1)求![]() (用
(用![]() 的表达式表示);
的表达式表示);
(2)垃圾发电厂该如何选址才能同时满足上述要求?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】函数![]() 图象上不同两点
图象上不同两点![]() ,
,![]() ,
,![]() ,
,![]() 处的切线的斜率分别是
处的切线的斜率分别是![]() ,
,![]() ,规定
,规定![]() 叫曲线
叫曲线![]() 在点
在点![]() 与点
与点![]() 之间的“弯曲度”,给出以下命题:
之间的“弯曲度”,给出以下命题:
(1)函数![]() 图象上两点
图象上两点![]() 、
、![]() 的横坐标分别为1,2,则
的横坐标分别为1,2,则![]() ;
;
(2)存在这样的函数,图象上任意两点之间的“弯曲度”为常数;
(3)设点![]() 、
、![]() 是抛物线,
是抛物线,![]() 上不同的两点,则
上不同的两点,则![]() ;
;
(4)设曲线![]() 上不同两点
上不同两点![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() ,若
,若![]() 恒成立,则实数
恒成立,则实数![]() 的取值范围是
的取值范围是![]() ;
;
以上正确命题的序号为__(写出所有正确的)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)的图象向左平移1个单位后关于y轴对称,当x2>x1>1时,[f(x2)﹣f(x1)](x2﹣x1)<0恒成立,设a=f(![]() ),b=f(2),c=f(3),则a、b、c的大小关系为( )
),b=f(2),c=f(3),则a、b、c的大小关系为( )
A.c>a>bB.c>b>aC.a>c>bD.b>a>c
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln (x+1)-![]() -x,a∈R.
-x,a∈R.
(1)当a>0时,求函数f(x)的单调区间;
(2)若存在x>0,使f(x)+x+1<-![]() (a∈Z)成立,求a的最小值.
(a∈Z)成立,求a的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出下列六个命题:
(1)若![]() ,则函数
,则函数![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(2)![]() 与
与![]() 的图像关于直线
的图像关于直线![]() 对称.
对称.
(3)![]() 的反函数与
的反函数与![]() 是相同的函数.
是相同的函数.
(4)![]() 无最大值也无最小值.
无最大值也无最小值.
(5)![]() 的最小正周期为
的最小正周期为![]() .
.
(6)![]() 有对称轴两条,对称中心有三个.
有对称轴两条,对称中心有三个.
则正确命题的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数![]() ,
,![]() .
.
(1)当![]() 时,求函数
时,求函数![]() 在点
在点![]() 处的切线方程;
处的切线方程;
(2)![]() 是函数
是函数![]() 的极值点,求函数
的极值点,求函数![]() 的单调区间;
的单调区间;
(3)在(2)的条件下,![]() ,若
,若![]() ,
,![]() ,使不等式
,使不等式![]() 恒成立,求
恒成立,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com