
分析 通过设弦的端点为A(x1,y1)、B(x2,y2),代入椭圆方程并相减,结合AB中点P的坐标计算即得结论.
解答 解:设弦的端点为A(x1,y1)、B(x2,y2),
则$\frac{{{x}_{1}}^{2}}{12}+\frac{{{y}_{1}}^{2}}{9}=1$、$\frac{{{x}_{2}}^{2}}{12}+\frac{{{y}_{2}}^{2}}{9}=1$,
两式相减并化简得:$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3}{4}$×$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$,
∵x1+x2=4、y1+y2=2,
∴k=$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{3}{2}$,
∴以P为中点的弦所在的直线方程为:y-1=-$\frac{3}{2}$(x-2),
化简得:3x+2y-8=0,
故答案为:3x+2y-8=0.
点评 本题考查直线与圆锥曲线的关系,注意解题方法的积累,属于基础题.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
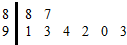 若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )
若某市8所中学参加中学生比赛的得分用茎叶图表示(如图)其中茎为十位数,叶为个位数,则这组数据的平均数和方差分别是( )| A. | 91 5.5 | B. | 91 5 | C. | 92 5.5 | D. | 92 5 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
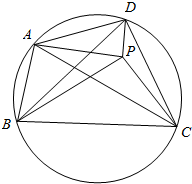 在凸四边形ABCD中,对角线BD不平分对角中的任意一个.点P在四边形ABCD内部,并且满足∠PBC=∠DBA和∠PDC=∠BDA.若A,B,C,D四点共圆,证明:AP=CP.
在凸四边形ABCD中,对角线BD不平分对角中的任意一个.点P在四边形ABCD内部,并且满足∠PBC=∠DBA和∠PDC=∠BDA.若A,B,C,D四点共圆,证明:AP=CP.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 32 | B. | 16 | C. | 8 | D. | 7 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com