
【题目】定义函数![]() ,
,![]() (0,
(0,![]() )为
)为![]() 型函数,共中
型函数,共中![]() .
.
(1)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 的值域;
的值域;
(2)若![]() 是
是![]() 型函数,求函数
型函数,求函数![]() 极值点个数;
极值点个数;
(3)若![]() 是
是![]() 型函数,在
型函数,在![]() 上有三点A、B、C横坐标分別为
上有三点A、B、C横坐标分別为![]() 、
、![]() 、
、![]() ,其中
,其中![]() <
<![]() <
<![]() ,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
,试判断直线AB的斜率与直线BC的斜率的大小并说明理由.
【答案】(1)![]() ;(2)1个;(3)见解析.
;(2)1个;(3)见解析.
【解析】
(1)先对函数求导求出其单调性,结合端点值求出值域;(2)先求导令导数等于0,求极值点个数只需判断导数零点的个数,化简整理后得![]() ,将导数零点转化为两个函数的交点问题,利用图像观察求出交点个数;(3)先求导再进行二阶求导,利用二阶导数研究一阶导数的单调性与范围,再得出原函数的单调性,因为二阶导数小于0,所以函数是三凸的单调递减函数,结合函数图像很容易得出两直线斜率的关系.
,将导数零点转化为两个函数的交点问题,利用图像观察求出交点个数;(3)先求导再进行二阶求导,利用二阶导数研究一阶导数的单调性与范围,再得出原函数的单调性,因为二阶导数小于0,所以函数是三凸的单调递减函数,结合函数图像很容易得出两直线斜率的关系.
解:(1)因为![]() ,
,![]()
所以![]()
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
又因为![]() ,
,![]() ,
,![]()
所以函数![]() 的值域为
的值域为![]()
(2)因为![]() ,
,![]()
所以![]() ,
,
当![]() 时,
时,![]()
结合函数图像易知![]() 与
与![]() 在
在![]() 上有且只有一个交点
上有且只有一个交点![]()
当![]() ,时
,时![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]()
当![]() 时,
时,![]() ,
,![]() ,
,![]()
且当![]() 时,
时,![]()
当![]() 时,
时,![]() ,函数
,函数![]() 单调递增
单调递增
当![]() 时,
时,![]() ,函数
,函数![]() 单调递减
单调递减
所以函数![]() 只有一个极大值点,极值点个数为1个
只有一个极大值点,极值点个数为1个
(3)因为![]() ,
,![]()
所以![]()
所以![]()
所以![]() 在
在![]() 上单调递减,且
上单调递减,且![]() ,所以
,所以![]()
构造函数![]() ,
,![]()
则![]()
记![]() ,
,![]()
则![]()
当![]() 时,
时,![]() ,
,![]() 单调递增
单调递增
当![]() 时,
时,![]() ,
,![]() 单调递减
单调递减
又因为![]() ,所以
,所以![]() ,所以
,所以![]()
所以![]() 在
在![]() 和
和![]() 上单调递减
上单调递减
因为![]() <
<![]() <
<![]()
所以![]()
所以![]()
所以直线AB的斜率大于直线BC的斜率


 53天天练系列答案
53天天练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的离心率
的离心率![]() ,右焦点
,右焦点![]() ,过点
,过点 的直线交椭圆
的直线交椭圆![]() 于
于![]() 两点.
两点.
(1)求椭圆![]() 的方程;
的方程;
(2)若点![]() 关于
关于![]() 轴的对称点为
轴的对称点为![]() ,求证:
,求证: ![]() 三点共线;
三点共线;
(3) 当![]() 面积最大时,求直线
面积最大时,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设P是抛物线y2=4x上的一个动点,F为抛物线的焦点,记点P到点A(-1,1)的距离与点P到直线x= - 1的距离之和的最小值为M,若B(3,2),记|PB|+|PF|的最小值为N,则M+N= ______________
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图1为某省2018年1~4月快递业务量统计图,图2是该省2018年1~4月快递业务收入统计图,下列对统计图理解错误的是( )


A. 2018年1~4月的业务量,3月最高,2月最低,差值接近2000万件
B. 2018年1~4月的业务量同比增长率均超过50%,在3月底最高
C. 从两图来看,2018年1~4月中的同一个月的快递业务量与收入的同比增长率并不完全一致
D. 从1~4月来看,该省在2018年快递业务收入同比增长率逐月增长
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某购物网站对在7座城市的线下体验店的广告费指出![]() 万元和销售额
万元和销售额![]() 万元的数据统计如下表:
万元的数据统计如下表:
城市 | A | B | C | D | E | F | G |
广告费支出 | 1 | 2 | 4 | 6 | 11 | 13 | 19 |
销售额 | 19 | 32 | 40 | 44 | 52 | 53 | 54 |
(1)若用线性回归模型拟合y与x关系,求y关于x的线性回归方程.
(2)若用对数函数回归模型拟合y与x的关系,可得回归方程![]() ,经计算对数函数回归模型的相关指数约为0.95,请说明选择哪个回归模型更合适,并用此模型预测A城市的广告费用支出8万元时的销售额.
,经计算对数函数回归模型的相关指数约为0.95,请说明选择哪个回归模型更合适,并用此模型预测A城市的广告费用支出8万元时的销售额.
参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
参考公式: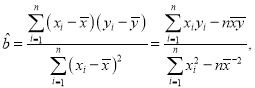
![]() ,
,
相关指数: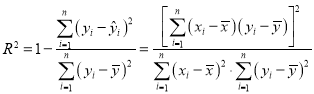 (注意:
(注意:![]() 与
与![]() 公式中的相似之处)
公式中的相似之处)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点.
的左、右焦点.
(1)若![]() 是该椭圆上的一个动点,求
是该椭圆上的一个动点,求![]() 的最大值和最小值;
的最大值和最小值;
(2)设过定点![]() 的直线
的直线![]() 与椭圆交于不同的两点
与椭圆交于不同的两点![]() ,且
,且![]() 为锐角(其中
为锐角(其中![]() 为坐标原点),求直线
为坐标原点),求直线![]() 的斜率的取值范围.
的斜率的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】下列命题:
①若将一组样本数据中的每个数据都加上同一个常数后,则样本的方差不变;
②在残差图中,残差点分布的带状区域的宽度越狭窄,其模型拟合的精度越高;
③若两个变量间的线性相关关系越强,则相关系数![]() 的值越接近于1;
的值越接近于1;
④对分类变量![]() 与
与![]() 的随机变量
的随机变量![]() 的观测值
的观测值![]() 来说,
来说,![]() 越小,判断“
越小,判断“![]() 与
与![]() 有关系”的把握越大.
有关系”的把握越大.
其中正确的命题序号是( )
A.①②③B.①②C.①③④D.②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com