
【题目】已知![]() 是数列
是数列![]() 的前
的前![]() 项和,对任意
项和,对任意![]() ,都有
,都有![]() ;
;
(1)若![]() ,求证:数列
,求证:数列![]() 是等差数列,并求此时数列
是等差数列,并求此时数列![]() 的通项公式;
的通项公式;
(2)若![]() ,求证:数列
,求证:数列![]() 是等比数列,并求此时数列
是等比数列,并求此时数列![]() 的通项公式;
的通项公式;
(3)设![]() ,若
,若![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
【答案】(1)证明见解析,![]() ;(2)
;(2)![]() ;(3)
;(3)![]() .
.
【解析】
(1)将![]() 代入
代入![]() ,得
,得![]() ,令
,令![]() ,求出
,求出![]() ,然后令
,然后令![]() ,由
,由![]() 得出
得出![]() ,两式作差可得出数列
,两式作差可得出数列![]() 的递推公式,然后利用定义证明出数列
的递推公式,然后利用定义证明出数列![]() 是等差数列,确定该数列的首项,即可求出
是等差数列,确定该数列的首项,即可求出![]() ;
;
(2)令![]() 求出
求出![]() ,然后令
,然后令![]() ,由
,由![]() 得出
得出![]() ,两式相减得出数列
,两式相减得出数列![]() 的递推公式,然后利用定义证明出数列
的递推公式,然后利用定义证明出数列![]() 为等比数列,确定该数列的首项和公比,即可求出
为等比数列,确定该数列的首项和公比,即可求出![]() ;
;
(3)结合(1)(2)中的结论,讨论![]() 、
、![]() 、
、![]() 、
、![]() 、
、![]() ,结合条件
,结合条件![]() ,利用数列
,利用数列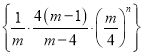 的单调性,即可得出实数
的单调性,即可得出实数![]() 的取值范围.
的取值范围.
(1)将![]() 代入
代入![]() ,得
,得![]() ,即
,即![]() .
.
当![]() 时,则有
时,则有![]() ,得
,得![]() ;
;
当![]() 时, 由
时, 由![]() 得出
得出![]() ,
,
上述两式相减得![]() ,
,
整理得![]() ,等式两边同时除以
,等式两边同时除以![]() 得
得![]() ,即
,即![]() ,
,
所以,数列![]() 是以首项为
是以首项为![]() 为首项,以
为首项,以![]() 为公差的等差数列,
为公差的等差数列,
则![]() ,因此,
,因此,![]() ;
;
(2)对任意![]() ,都有
,都有![]() .
.
当![]() 时,
时,![]() ,解得
,解得![]() ;
;
当![]() 时,由
时,由![]() 得出
得出![]() ,
,
两式相减得![]() ,
,
化简得![]() ,
,
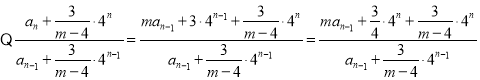
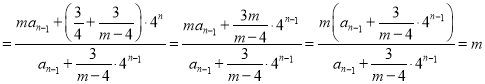 ,
,
所以,数列![]() 是以
是以![]() 为公比,以
为公比,以![]() 为首项的等比数列,则
为首项的等比数列,则![]() ,因此,
,因此,![]() ;
;
(3)![]() ,且
,且![]() .
.
当![]() 时,
时,![]() ,当
,当![]() 时,
时,![]() ,不满足条件;
,不满足条件;
则![]() ,可得
,可得![]() ,
,
可得![]() ,
,
显然![]() 时,数列
时,数列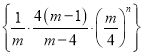 单调递增,不满足条件,
单调递增,不满足条件,![]() .
.
当![]() 时,则有
时,则有![]() 显然成立;
显然成立;
当![]() 时,若
时,若![]() ,则数列
,则数列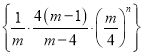 的最大项为
的最大项为![]() ,
,
![]() ,即
,即![]() 恒成立;
恒成立;
当![]() 时,数列
时,数列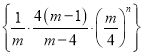 的最大项为
的最大项为![]() ,
,
则![]() 满足条件;
满足条件;
当![]() 时,
时,![]() ,数列
,数列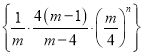 的最大项为
的最大项为![]() ,不满足条件;
,不满足条件;
综上所述,实数![]() 的取值范围是
的取值范围是![]() .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
【题目】共有编号分别为1,2,3,4,5的五个座位,在甲同学不坐2号座位,乙同学不坐5号座位的条件下,甲、乙两位同学的座位号相加是偶数的概率为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
: ![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,且
,且![]() 与短轴的一个端点Q构成一个等腰直角三角形,点P(
与短轴的一个端点Q构成一个等腰直角三角形,点P(![]() )在椭圆
)在椭圆![]() 上,过点
上,过点![]() 作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆
作互相垂直且与x轴不重合的两直线AB,CD分别交椭圆![]() 于A,B,C,D且M,N分别是弦AB,CD的中点
于A,B,C,D且M,N分别是弦AB,CD的中点
(1)求椭圆的方程
(2)求证:直线MN过定点R(![]() )
)
(3)求![]() 面积的最大值
面积的最大值
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知数列![]() 与
与![]() 满足
满足![]() .
.
(1)若![]() ,求数列
,求数列![]() 的通项公式;
的通项公式;
(2)若![]() 且数列
且数列![]() 为公比不为1的等比数列,求q的值,使数列
为公比不为1的等比数列,求q的值,使数列![]() 也是等比数列;
也是等比数列;
(3)若![]() 且
且![]() ,数列
,数列![]() 有最大值M与最小值
有最大值M与最小值![]() ,求
,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,曲线
中,曲线![]() 的参数方程为
的参数方程为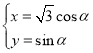 ,其中
,其中![]() 为参数,
为参数,![]() .在以坐标原点
.在以坐标原点![]() 为极点,轴的正半轴为极轴的极坐标系中,点
为极点,轴的正半轴为极轴的极坐标系中,点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求直线![]() 的直角坐标方程与曲线
的直角坐标方程与曲线![]() 的普通方程;
的普通方程;
(2)若![]() 是曲线
是曲线![]() 上的动点,
上的动点,![]() 为线段
为线段![]() 的中点.求点
的中点.求点![]() 到直线
到直线![]() 的距离的最大值.
的距离的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知![]() 是公差为
是公差为![]() 的等差数列,
的等差数列,![]() 是公比为
是公比为![]() 的等比数列.
的等比数列.
(1)若![]() ,是否存在
,是否存在![]() ,有
,有![]() ?请说明理由;
?请说明理由;
(2)若![]() (
(![]() 、
、![]() 为常数,且
为常数,且![]() )对任意
)对任意![]() ,有
,有![]() ,试求出
,试求出![]() 、
、![]() 满足的充要条件;
满足的充要条件;
(3)若![]() ,
,![]() ,试确定所有
,试确定所有![]() ,使数列
,使数列![]() 中存在某个连续
中存在某个连续![]() 项的和是数列
项的和是数列![]() 中的一项,请证明.
中的一项,请证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在四棱锥P—ABCD中,![]() PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.
PAB为正三角形,四边形ABCD为炬形,平面PAB⊥平面ABCD.AB=2AD,M,N分别为PB,PC中点.

(1)求证:MN//平面PAD;
(2)求二面角B—AM—C的大小;
(3)在BC上是否存在点E,使得EN⊥平面AMV?若存在,求![]() 的值:若不存在,请说明理由.
的值:若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某国际性会议纪念章的一特许专营店销售纪念章,每枚进价为5元,同时每销售一枚这种纪念章还需向该会议的组织委员会交特许经营管理费2元,预计这种纪念章以每枚20元的价格销售时,该店一年可销售2000枚,经过市场调研发现,每枚纪念章的销售价格在每枚20元的基础上,每减少一元则增加销售400枚,而每增加一元则减少销售100枚,现设每枚纪念章的销售价格为![]() 元(每枚的销售价格应为正整数).
元(每枚的销售价格应为正整数).
(1)写出该特许专营店一年内销售这种纪念章所获得的利润![]() (元)与每枚纪念章的销售价格
(元)与每枚纪念章的销售价格![]() 的函数关系式;
的函数关系式;
(2)当每枚纪念章销售价格![]() 为多少元时,该特许专营店一年内利润
为多少元时,该特许专营店一年内利润![]() (元)最大,并求出这个最大值;
(元)最大,并求出这个最大值;
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com