
已知直线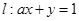 在矩阵
在矩阵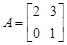 对应的变换作用下变为直线
对应的变换作用下变为直线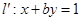 .
.
(1)求实数 ,
, 的值;
的值;
(2)若点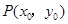 在直线
在直线 上,且
上,且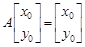 ,求点
,求点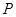 的坐标.
的坐标.
 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:填空题
对于 个互异的实数,可以排成
个互异的实数,可以排成 行
行 列的矩形数阵,右图所示的
列的矩形数阵,右图所示的 行
行 列的矩形数阵就是其中之一.将
列的矩形数阵就是其中之一.将 个互异的实数排成
个互异的实数排成 行
行 列的矩形数阵后,把每行中最大的数选出,记为
列的矩形数阵后,把每行中最大的数选出,记为 ,并设其中最小的数为
,并设其中最小的数为 ;把每列中最小的数选出,记为
;把每列中最小的数选出,记为 ,并设其中最大的数为
,并设其中最大的数为 .
.
两位同学通过各自的探究,分别得出两个结论如下:
① 和
和 必相等; ②
必相等; ② 和
和 可能相等;
可能相等;
③ 可能大于
可能大于 ; ④
; ④ 可能大于
可能大于 .
.
以上四个结论中,正确结论的序号是__________________(请写出所有正确结论的序号).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知在矩阵M对应的变换作用下,点A(1,0)变为A′(1,0),点B(1,1)变为B′(2,1).
(1)求矩阵M;
(2)求 ,
, ,并猜测
,并猜测 (只写结果,不必证明).
(只写结果,不必证明).
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在平面直角坐标系中,一种线性变换对应的2×2矩阵为 .
.
(1)求点A( ,3)在该变换作用下的象.
,3)在该变换作用下的象.
(2)求圆x2+y2=1在该变换作用下的新曲线的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
在直角坐标系中,△OAB的顶点坐标O(0,0)、A(2,0),B(1, ),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M=
),求△OAB在矩阵MN的作用下变换所得到的图形的面积,其中矩阵M= ,N=
,N= .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com