
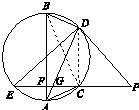
【题目】如图所示,EP交圆于E,C两点,PD切圆于D,G为CE上一点且PG=PD,连接DG并延长交圆于点A,作弦AB垂直EP,垂足为F. 
(1)求证:BD⊥AD;
(2)若AC=BD,AB=6,求弦DE的长.
【答案】
(1)证明:∵PG=PD,∴∠PDG=∠PGD,
由于PD为切线,故∠PDA=∠DBA,
又∵∠EGA=∠PGD,∴∠EGA=∠DBA,
∴∠DBA+∠BAD=∠EGA+∠BAD,
从而∠PFA=∠BDA.
又AF⊥EP,∴∠PFA=90°,则∠BDA=90°,
故AB为圆的直径,
∴BD⊥AD.
(2)解:连接BC,DC.
由于AB是直径,故∠BDA=∠ACB=90°.
在Rt△BDA与Rt△ACB中,AB=BA,AC=BD,从而得Rt△BDA≌Rt△ACB,
于是∠DAB=∠CBA.
又∵∠DCB=∠DAB,∴∠DCB=∠CBA,故DC∥AB.
∵AB⊥EP,∴DC⊥EP,∠DCE为直角,
∴ED为直径,又由(1)知AB为圆的直径,
∴DE=AB=6
【解析】(1)由已知PG=PD,得到∠PDG=∠PGD,由切割弦定理得到∠PDA=∠DBA,进一步得到∠EGA=∠DBA,从而∠PFA=∠BDA.最后可得∠BDA=90°,说明AB为圆的直径;(2)连接BC,DC.由AB是直径得到∠BDA=∠ACB=90°,然后由Rt△BDA≌Rt△ACB,得到∠DAB=∠CBA.再由∠DCB=∠DAB可推得DC∥AB.进一步得到ED为直径,则ED长可求.


科目:高中数学 来源: 题型:
【题目】《九章算术》中有如下问题:今有蒲生一日,长三尺,莞生一日,长1尺.蒲生日自半,莞生日自倍.问几何日而长等?意思是:今有蒲第一天长高3尺,莞第一天长高1尺,以后蒲每天长高前一天的一半,莞每天长高前一天的2倍.若蒲、莞长度相等,则所需时间为( )
(结果精确到0.1.参考数据:lg2=0.3010,lg3=0.4771.)
A. ![]() 天B.
天B. ![]() 天C.
天C. ![]() 天D.
天D. ![]() 天
天
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某家具厂有方木料90![]() ,五合板600
,五合板600![]() ,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l
,准备加工成书桌和书橱出售.已知生产第张书桌需要方木料O.l![]() ,五合板2
,五合板2![]() ,生产每个书橱而要方木料0.2
,生产每个书橱而要方木料0.2![]() ,五合板1
,五合板1![]() ,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
,出售一张方桌可获利润80元,出售一个书橱可获利润120元.
(1)如果只安排生产书桌,可获利润多少?
(2)怎样安排生产可使所得利润最大?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆心在![]() 轴的正半轴上,且半径为2的圆
轴的正半轴上,且半径为2的圆![]() 被直线
被直线![]() 截得的弦长为
截得的弦长为![]() .
.
(1)求圆![]() 的方程;
的方程;
(2)设动直线![]() 与圆
与圆![]() 交于
交于![]() 两点,则在
两点,则在![]() 轴正半轴上是否存在定点
轴正半轴上是否存在定点![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于
关于![]() 轴对称?若存在,请求出点
轴对称?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知极坐标系的极点与直角坐标系的原点重合,极轴与x轴的非负半轴重合,若曲线C1的方程为ρsin(θ+ ![]() )+2
)+2 ![]() =0,曲线C2的参数方程为
=0,曲线C2的参数方程为 ![]() (θ为参数).
(θ为参数).
(1)将C1的方程化为直角坐标方程;
(2)若点Q为C2上的动点,P为C1上的动点,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】土笋冻是闽南种广受欢迎的特色传统风味小吃某小区超市销售一款土笋冻,进价为每个15元,售价为每个20元.销售的方案是当天进货,当天销售,未售出的全部由厂家以每个10元的价格回购处理.根据该小区以往的销售情况,得到如图所示的频率分布直方图:

(1)估算该小区土笋冻日需求量的平均数![]() (同一组中的数据用该组区间的中点值代表);
(同一组中的数据用该组区间的中点值代表);
(2)已知该超市某天购进了150个土笋冻,假设当天的需求量为![]() 个
个![]() 销售利润为
销售利润为![]() 元.
元.
(i)求关于![]() 的函数关系式;
的函数关系式;
(ii)结合上述频率分布直方图,以额率估计概率的思想,估计当天利润![]() 不小于650元的概率.
不小于650元的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥P-ABCD中,AB//CD,且![]() .
.

(1)证明:平面PAB⊥平面PAD;
(2)若PA=PD=AB=DC, ![]() ,求二面角A-PB-C的余弦值.
,求二面角A-PB-C的余弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com