
设定义在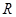 上的函数
上的函数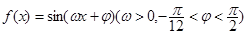 ,给出以下四个论断:
,给出以下四个论断:
①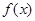 的周期为π;
②
的周期为π;
②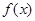 在区间(
在区间(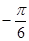 ,0)上是增函数;
,0)上是增函数;
③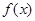 的图象关于点(
的图象关于点(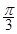 ,0)对称;④
,0)对称;④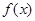 的图象关于直线
的图象关于直线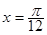 对称.
对称.
以其中两个论断作为条件,另两个论断作为结论,写出你认为正确的一个命题(写成“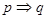 ”的形式): (其中用到的论断都用序号表示)
”的形式): (其中用到的论断都用序号表示)
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案科目:高中数学 来源: 题型:044
(
南通中学模拟)设定义在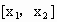 上的函数y=f(x)的图象为C,C的端点为点A、B,M是C上的任意一点,向量
上的函数y=f(x)的图象为C,C的端点为点A、B,M是C上的任意一点,向量

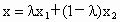 ,记向量
,记向量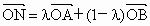 .现在定义“函数y=f(x)在
.现在定义“函数y=f(x)在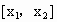 上可在标准k下线性近似”是指
上可在标准k下线性近似”是指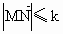 恒成立,其中k是一个人为确定的正数.
恒成立,其中k是一个人为确定的正数.
(1)
证明:0≤λ≤1;(2)
请你给出一个标准k的范围,使得[0,1]上的函数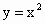 与
与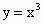 中有且只有一个可在标准k下线性近似.
中有且只有一个可在标准k下线性近似.查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省资阳市二下学期期末质量检测理科数学试卷(解析版) 题型:填空题
给出以下四个命题:
①动点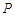 到两定点
到两定点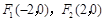 的距离之和为4,则点
的距离之和为4,则点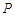 的轨迹为椭圆;
的轨迹为椭圆;
②设定义在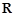 上的可导函数
上的可导函数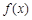 满足
满足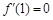 ,
, ,则
,则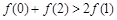 一定成立;
一定成立;
③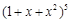 展开式中,含
展开式中,含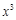 项的系数为30;
项的系数为30;
④若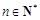 ,则
,则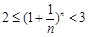 .
.
其中,所有真命题的序号为 .
查看答案和解析>>
科目:高中数学 来源:2011-2012学年四川省高三第6次月考理科数学试卷(解析版) 题型:填空题
若函数 在给定区间M上存在正数t,使得对于任意
在给定区间M上存在正数t,使得对于任意 ,有
,有 ,且
,且 ,则称
,则称 为M上的t级类增函数。给出4个命题
为M上的t级类增函数。给出4个命题
①函数 上的3级类增函数
上的3级类增函数
②函数 上的1级类增函数
上的1级类增函数
③若函数 上的
上的 级类增函数,则实数a的最小值为2
级类增函数,则实数a的最小值为2
④设 是定义
是定义 在上的函数,且满足:1.对任意
在上的函数,且满足:1.对任意 ,恒有
,恒有 ;2.对任意
;2.对任意 ,恒有
,恒有 ;3. 对任意
;3. 对任意 ,
, ,若函数
,若函数 是
是 上的t级类增函数,则实数t的取值范围为
上的t级类增函数,则实数t的取值范围为 。
。
以上命题中为真命题的是
查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省高三上学期期末理科数学试卷 题型:解答题
已知函数 其中常数
其中常数
(1)当 时,求函数
时,求函数 的单调递增区间;
的单调递增区间;
(2)当 时,给出两类直线:
时,给出两类直线: 与
与 ,其中
,其中 为常数,判断这两类直线中是否存在
为常数,判断这两类直线中是否存在 的切线,若存在,求出相应的
的切线,若存在,求出相应的 或
或 的值,若不存在,说明理由.
的值,若不存在,说明理由.
(3)设定义在 上的函数
上的函数 在点
在点 处的切线方程为
处的切线方程为 ,当
,当 若
若 在
在 内恒成立,则称
内恒成立,则称 为函数
为函数 的“类对称点”,当
的“类对称点”,当 时,试问
时,试问 是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标,若不存在,说明理由.
是否存在“类对称点”,若存在,请至少求出一个“类对称点”的横坐标,若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com