
【题目】如图,在棱台![]() 中,
中, ![]() 与
与![]() 分别是棱长为1与2的正三角形,平面
分别是棱长为1与2的正三角形,平面![]() 平面
平面![]() ,四边形
,四边形![]() 为直角梯形,
为直角梯形, ![]() ,
, ![]() ,
, ![]() 为
为![]() 中点,
中点, ![]() (
(![]() ,
, ![]() ).
).

(1)设![]() 中点为
中点为![]() ,
, ![]() ,求证:
,求证: ![]() 平面
平面![]() ;
;
(2)若![]() 到平面
到平面![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
【答案】(1)见解析(2)![]()
【解析】试题分析:(1)延长三棱台![]() 的三条侧棱,设交点为
的三条侧棱,设交点为![]() ,
, ![]() 时
时![]() 为
为![]() 的中点,设
的中点,设![]() 中点为
中点为![]() ,连
,连![]() 梯形
梯形![]() 中,中位线
中,中位线![]() ,根据线面平行的判定定理可得
,根据线面平行的判定定理可得![]() 平面
平面![]() ;同理可证
;同理可证![]() 平面
平面![]() ,然后再根据面面平行的判定定理可得,平面
,然后再根据面面平行的判定定理可得,平面![]() 平面
平面![]() ,进而可证命题成立;(2)设
,进而可证命题成立;(2)设![]() 中点为
中点为![]() ,连
,连![]() ,在
,在![]() 中作
中作![]() 且交
且交![]() 于点
于点![]() ,由面面垂直的性质定理,可得
,由面面垂直的性质定理,可得![]() ,又
,又![]() ,所以
,所以![]() 平面
平面![]() ,所以
,所以![]() 为
为![]() 到平面
到平面![]() 的距离,
的距离, ![]()
且![]() 为直线
为直线![]() 与平面
与平面![]() 所成角;再根据面面垂直的性质定理,可得
所成角;再根据面面垂直的性质定理,可得![]() 可得
可得![]() ,
, ![]() 中
中![]() 为
为![]() 的中点
的中点![]()
![]() ,由此即可求出线面角的正弦值.
,由此即可求出线面角的正弦值.
试题解析:
(1)延长三棱台![]() 的三条侧棱,设交点为
的三条侧棱,设交点为![]()
![]() 时
时![]() 为
为![]() 的中点,
的中点,
设![]() 中点为
中点为![]() ,连
,连![]()
梯形![]() 中,中位线
中,中位线![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]() ;
;
![]() 中,中位线
中,中位线![]() ,又
,又![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以![]() 平面
平面![]()
又![]() 且
且![]() 平面
平面![]() ,
, ![]() 平面
平面![]()
所以平面![]() 平面
平面![]()
所以![]() 平面
平面![]()
(2)设![]() 中点为
中点为![]() ,连
,连![]() ,在
,在![]() 中作
中作![]() 且交
且交![]() 于点
于点![]() ,
,

又![]() ,所以
,所以![]() 平面
平面![]() ,
,
所以![]() 为
为![]() 到平面
到平面![]() 的距离,
的距离, ![]()
且![]() 为直线
为直线![]() 与平面
与平面![]() 所成角
所成角

![]() 平面
平面![]() ,所以
,所以![]() ,
, ![]() 中
中![]()
 为
为![]() 的中点
的中点
![]()
![]()
直线![]() 与平面
与平面![]() 所成角的正弦值为
所成角的正弦值为![]() .
.


科目:高中数学 来源: 题型:
【题目】甲、乙两位学生参加数学竞赛培训,在培训期间他们参加的5次预寒成绩记录如下:
甲:82,82,79,95,87
乙:95,75,80,90,85
(1)用茎叶图表示这两组数据;
(2)求甲、乙两人成绩的平均数与方差;
(3)若现要从中选派一人参加数学竞赛,你认为选派哪位学生参加合适,说明理由?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x﹣cosx,{an}是公差为 ![]() 的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
的等差数列,f(a1)+f(a2)+…+f(a5)=5π,则[f(a3)]2﹣a1a5=( )
A.0
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,四棱锥![]() 中,
中, ![]() 底面
底面![]() ,底面
,底面![]() 是直角梯形,
是直角梯形, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,点
,点![]() 在
在![]() 上,且
上,且![]() .
.
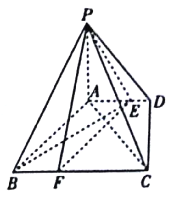
(Ⅰ)已知点![]() 在
在![]() 上,且
上,且![]() ,求证:平面
,求证:平面![]() 平面
平面![]() ;
;
(Ⅱ)当二面角![]() 的余弦值为多少时,直线
的余弦值为多少时,直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ?
?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】己知在平面直角坐标系![]() 中,圆
中,圆![]() 的参数方程为
的参数方程为 (
(![]() 为参数)以
为参数)以![]() 轴为极轴,
轴为极轴, ![]() 为极点建立极坐标系,在该极坐标系下,圆
为极点建立极坐标系,在该极坐标系下,圆![]() 是以点
是以点![]() 为圆心,且过点
为圆心,且过点![]() 的圆心.
的圆心.
(1)求圆![]() 及圆
及圆![]() 在平而直角坐标系
在平而直角坐标系![]() 下的直角坐标方程;
下的直角坐标方程;
(2)求圆![]() 上任一点
上任一点![]() 与圆
与圆![]() 上任一点之间距离的最小值.
上任一点之间距离的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】教育学家分析发现加强语文乐队理解训练与提高数学应用题得分率有关,某校兴趣小组为了验证这个结论,从该校选择甲乙两个同轨班级进行试验,其中甲班加强阅读理解训练,乙班常规教学无额外训练,一段时间后进行数学应用题测试,统计数据情况如下面的![]() 列联表(单位:人)
列联表(单位:人)

(1)能够据此判断有97.5%把握热内加强语文阅读训练与提高数学应用题得分率有关?
(2)经过多次测试后,小明正确解答一道数学应用题所用的时间在5—7分钟,小刚正确解得一道数学应用题所用的时间在6—8分钟,现小明、小刚同时独立解答同一道数学应用题,求小刚比小明现正确解答完的概率;

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50m/min.在甲出发2min后,乙从A乘缆车到B,在B处停留1min后,再从B匀速步行到C.假设缆车匀速直线运动的速度为130m/min,山路AC长为1260m,经测量,cosA= ![]() ,cosC=
,cosC= ![]()
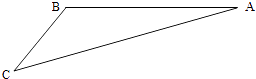
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com